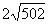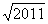- 直线与抛物线的位置关系
- 共49题
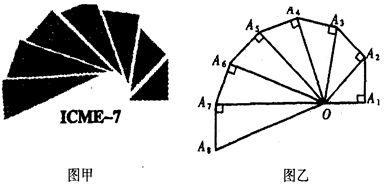
如图甲是第七届国际数学教育大会（简称ICME—7）的会徽图案，会徽的主体图案是由
如图乙的一连串直角三角形演化而成的，其中OA1=A1A2=A2A3=…A7A8=1，如果把图乙中的直
角三角形继续作下去，记OA1，OA2，…，OAn，…的长度构成数列{an}，则a2011=(
A2008
B50
C
D
正确答案
解析
略
知识点
集合
A
B
C
D
正确答案
解析
略
知识点
设曲线
的部分有两个交点，则实数
正确答案
见解析
解析
易知直线
直线
故应有：
知识点
抛物线
A
B
C
D
正确答案
解析
略
知识点
如图6，已知点
（1）求
（2）已知抛物线C的顶点为原点O，焦点在
正确答案
见解析。
解析
（1）
设点
于是
当且仅当A、P、B三点共线是取等号，
这时|PA|+|PB|取得最小值
（2）解法一：依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
过点M作y轴的垂线，垂足为G，则点G平分DE，
设圆心为M(m，n)，
则
即当M运动时，弦DE的长不随圆心M的变化而变化，
又∵点A'到y轴的距离不变，∴三角形A'DE的面积不随圆心M的变化而变化，
解法二：依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
设圆的圆心为
∴圆的方程为
令
∵点
设
则
即当M运动时，弦DE的长不随圆心M的变化而变化，
又∵点A'到y轴的距离不变，∴三角形A'DE的面积不随圆心M的变化而变化；
解法三：依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
设圆的圆心为
∴圆的方程为
令
∵点
设
由求根公式得
∴当M运动时，弦长|DE|为定值，
又∵点A'到y轴的距离不变，∴三角形A'DE的面积不随圆心M的变化而变化，
解法四：依题意知点
设抛物线C的方程为
由抛物线C过点B得
即抛物线C的方程为
设圆的圆心为
∴圆的方程为
令
设
则
又∵点
∴当M运动时，弦长|DE|为定值，又∵点A'到y轴的距离不变，
∴三角形A'DE的面积不随圆心M的变化而变化，
知识点
扫码查看完整答案与解析