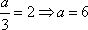热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知数列是无穷等比数列，其前n项和是，若，，则的值为........................................................................( )

正确答案

解析

略

知识点

数列的极限

题型：填空题

填空题 · 4 分

设，的二项展开式中含项的系数为7，则____。

正确答案

解析

略

知识点

数列的极限求二项展开式的指定项或指定项的系数

题型：单选题

单选题 · 5 分

已知，则=

A-6

正确答案

解析

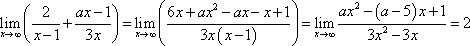
故

知识点

数列的极限

题型：单选题

单选题 · 5 分

（）

D不存在

正确答案

解析

考查等比数列求和与极限知识.解法一：先求和，然后对和取极限。

知识点

数列的极限

题型：单选题

单选题 · 5 分

对于具有相同定义域D的函数和,若存在函数为常数),对任给的正数m,存在相应的,使得当且时,总有,则称直线为曲线和的“分渐近线”.给出定义域均为D=的四组函数如下:

①, ; ②,;

③,; ④,.

其中, 曲线和存在“分渐近线”的是( )

A①④

B②③

C②④

D③④

正确答案

解析

要透过现象看本质，存在分渐近线的充要条件是时，。对于1，当时便不符合，所以1不存在；对于2，肯定存在分渐近线，因为当时，；对于3，，设且，所以当时越来愈大，从而会越来越小，不会趋近于0，所以不存在分渐近线；4当时，，因此存在分渐近线。故，存在分渐近线的是24

知识点

函数的值域数列的极限

继续学习学习下一知识点

下一知识点 : 数列与不等式的综合

百度题库 > 高考 > 理科数学 > 数列的极限

扫码查看完整答案与解析