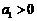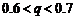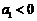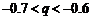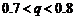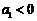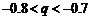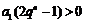- 数列的极限
- 共32题
1
题型:
单选题
|
17. 已知无穷等比数列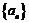
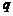
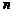
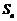
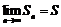
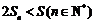
正确答案
B
解析
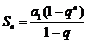
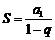
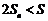
若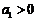
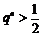
若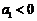
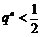
知识点
数列的极限
1
题型:简答题
|
已知


27.设



28.设






29.设





第(1)小题正确答案及相关解析
正确答案
(1)
解析
(1)因为

所以
进而
由已知可知

考查方向
本题主要考查函数的性质,能成立问题、极限的求法等知识,意在考查考生的分析问题、解决问题,转化与划归的能力。
解题思路
根据函数的单调性求出

易错点
1.错将能成立问题转化为恒成立问题处理;2.对于题中出现的字母太多导致无法入手。
第(2)小题正确答案及相关解析
正确答案
(2)略;
解析
(2)当

所以
进而


由于区间

所以

因此,
考查方向
本题主要考查函数的性质,能成立问题、极限的求法等知识,意在考查考生的分析问题、解决问题,转化与划归的能力。
解题思路
先根据题意确定
易错点
1.错将能成立问题转化为恒成立问题处理;2.对于题中出现的字母太多导致无法入手。
第(3)小题正确答案及相关解析
正确答案

解析
(3)由于
所以

进而
由题意对任意

当


当


综上,实数

考查方向
本题主要考查函数的性质,能成立问题、极限的求法等知识,意在考查考生的分析问题、解决问题,转化与划归的能力。
解题思路
先求出
易错点
1.错将能成立问题转化为恒成立问题处理;2.对于题中出现的字母太多导致无法入手。
下一知识点 : 数列与不等式的综合
扫码查看完整答案与解析