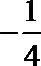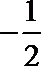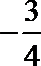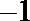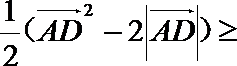- 向量在几何中的应用
- 共120题
已知正三角形ABC的边长为


正确答案
知识点
13.如图,在







正确答案

解析
令




则





则


由




因此
考查方向
解题思路
设出基向量,求出向量表达式,利用向量的关系通过转化求出数量积。
易错点
向量的线性转化运算。
知识点
18.如图,在平面直角坐标系


及其上一点
⑴ 设圆





⑵ 设平行于





⑶ 设点





正确答案
(1)因为



则圆

又圆



则



⑵ 由题意得





则


解得




⑶ 



又
即

对于任意

此时


必然与圆交于


因此对于任意
综上
知识点
8.O是平面上一定点,A、B、C平面上不共线的三点,动点P满足
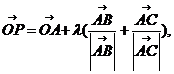
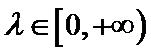
正确答案
解析
由已知可得
考查方向
解题思路
将已知的等式化简,根据向量共线基本定理找到AP是在三角形的角平分线上。
易错点
1、不能根据已知的等式将其化简。
知识点
14.在直角梯形中










正确答案
5
解析
由题可知,以A为原点建系,

F(1/λ,√3),所以
考查方向
解题思路
1、画出平面图形并利用坐标系分析;2、表示平面向量,即可得到结果。
易错点
本题易在表示平面向量时发生错误。
知识点
10. 在边长为2的正三角形ABC中,D为BC中点,点P是该等边三角形的三边上的动点,求
正确答案
解析
设AD的中点为O,那么

考查方向
解题思路
本题可以建立坐标系用向量建立函数关系,可以直接用向量点积的几何意义建立函数关系求解
易错点
容易选择D答案,选择两个端点检验。
知识点
3. 如图, 正方形




正确答案
解析
因为


考查方向
本题考查了平面向量的三角形法则,在近几年的各省高考题出现的频率较低.
解题思路
利用基向量

易错点
使用加法公式

知识点
11.已知菱形






正确答案
2
解析


考查方向
解题思路
本题考查运用平面向量在几何中的应用,解题步骤如下:建立如图所示直角坐标系,
则

易错点
本题必须注意审题,忽视则会出现错误。
知识点
正确答案
1
知识点
11.已知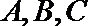
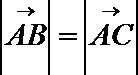
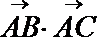
正确答案
解析
设: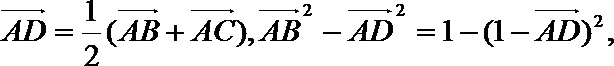
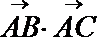
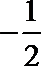
考查方向
本题主要考查平面向量
解题思路
(1)在单位圆中表示出向量;(2)利用圆的性质求解,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在化简时发生错误。
知识点
扫码查看完整答案与解析