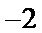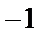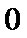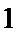向量在几何中的应用
共120题

· 向量在几何中的应用

向量在几何中的应用
共120题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

15.已知的重心为O，过O任做一直线分别交边AB，AC于P，Q两点，设，则的最小值是______.

正确答案

解析

如图所示

∵P，O，Q三点共线，则

∵的重心为O

∴

考查方向

本题主要考查了向量的几何意义以及三点共线定理、基本不等式

解题思路

先利用向量的几何意义，利用三点共线，得出的关系，然后利用基本不等式求解

易错点

本题不会利用三点共线转化

知识点

平面向量的基本定理及其意义向量在几何中的应用

题型：单选题

单选题 · 5 分

5.在平面直角坐标系中，为坐标原点，直线与圆相交于

两点，，若点在圆上，则实数（）

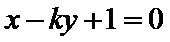
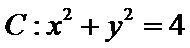
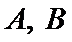
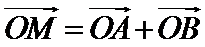
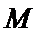
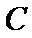
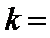
正确答案

解析

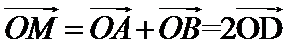
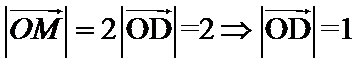
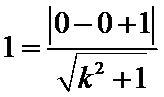
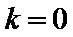
设AB中点为D，由知，由点到直线的距离公式得，解得，故选择C选项。

考查方向

本题主要考查了直线与圆的位置关系、平面向量的基本定理及其意义，为高考常考题，在近几年的各省高考题出现的频率较高，常与平面向量、圆的相关性质等知识点交汇命题。

解题思路

设AB中点为D，有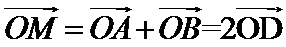，即圆心到直线的距离等于半径的一半，由点到直线的距离公式列方程即可求出k的值。

易错点

对已知条件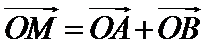不知如何应用。

知识点

向量在几何中的应用

题型：单选题

单选题 · 5 分

9.已知点A,B,C在圆上运动，且AB,若点P的坐标为（2，0）则的

最大值为

正确答案

解析

由题意得，AC为圆的直径，故可设，，，∴，而，∴的最大值为，故选B选项。

考查方向

本题主要考察圆的性质和平面向量数量积等知识，意在考察考生的数形结合能力和转化与划归的能力。

解题思路

先由题意得到AC为圆的直径，后设出所需要点的坐标后把所求的结果表示成函数的形式后求其最值即可。

易错点

1.不会转化题中的条件；2.不会利用坐标法解决问题。

知识点

向量在几何中的应用圆的标准方程

题型：填空题

填空题 · 5 分

11．如图，在中，，，，则的值为________.

正确答案

解析

说明D在线段BC上，且是靠近B的一个三等分点，以向量, 为一组基底，表示出向量的数量积，即可算出的值为。

考查方向

本题主要考查了平面向量的数量积,在近几年的各省高考题出现的频率较高，常与三角恒等变形公式，向量的运算等知识点交汇命题。

解题思路

平面向量的数量积计算问题，往往有两种形式，一种是数量积的定义，而是利用数量积的坐标运算公式，涉及几何图形的问题，可利用几何性质用一组已知基底数量积表示所求数量积。

易错点

1、本题易直接使用数量积的定义，而不知如何计算夹角。

2、不会选择一组基底，从而用向量的加减运算及利用几何性质用一组已知基底数量积表示所求数量积。

知识点

余弦定理平面向量数量积的运算向量在几何中的应用

题型：填空题

填空题 · 5 分

14．已知向量a＝（x－1，2），b＝（4，y），若a⊥b，则点P（x，y）到原点的距离的最小值为___________．

正确答案

；

解析

由已知得为。

考查方向

向量的数量积的坐标运算。

解题思路

本题考查向量数量积的坐标运算，根据已知得到一个二元一次方程，最后转化为原点到这条直线的距离来解答。

易错点

点p到原点的距离不知道怎么来解答。

知识点

数量积判断两个平面向量的垂直关系向量在几何中的应用

继续学习学习下一知识点

下一知识点 : 平面向量的综合题

百度题库 > 高考 > 文科数学 > 向量在几何中的应用

扫码查看完整答案与解析