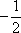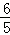- 向量在几何中的应用
- 共120题
在正三角形ABC中,D是BC上的点,AB=3,BD =1,则
正确答案
6
解析
知识点
在平面直角坐标系









正确答案
解析
略
知识点
已知P是以F1、F2为焦点的椭圆


正确答案
解析
由
∴
又知tan∠PF1F2 =
∴
而PF1 + PF2 = 2a,F1F2 = 2c
e =
知识点
已知




正确答案
解析
略
知识点
若向量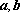
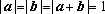
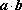
正确答案
解析
略
知识点
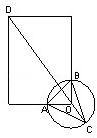
在四边形



正确答案
解析
略
知识点
△ABC内接于以O为圆心半径为1的圆,且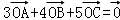
正确答案
解析
如图,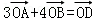
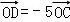
且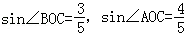
所以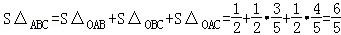
知识点
已知双曲线


正确答案
解析
由题意可得由题意得A(0,b),C(0,﹣b),B(﹣a,0),F(﹣c,0),
∴







知识点
已知椭圆



(1)求椭圆
(2)过椭圆









正确答案
(1)
解析
(1)解:设椭圆C的方程为


抛物线方程化为

则椭圆C的一个顶点为



所以椭圆C的标准方程为 
(2)证明:易求出椭圆C的右焦点
设

设直线


得 
∴

又,



而 

即
∴

所以 
知识点
椭圆



(1)求椭圆的方程;
(2)过




正确答案
(1)
(2)y=x-1或y=-x-1
解析
(1)设右焦点为




又离心率



故椭圆方程为
(2)设





易知当直线的斜率不存在或斜率为0时,①不成立,
于是设的方程为



因为
于是

由①③得,



所以直线的方程是

知识点
扫码查看完整答案与解析