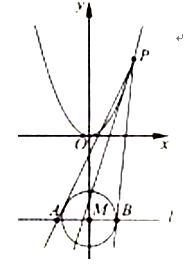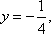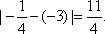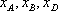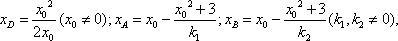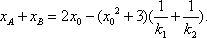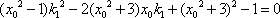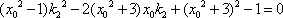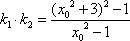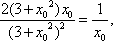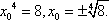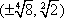- 导数的几何意义
- 共154题
已知函数
(1)若曲线




(2)若曲线


正确答案
(1)a=0,b=f(0)=1.
(2)(1,+∞)
解析
由f(x)=x2+xsin x+cos x,得f′(x)=x(2+cos x)。
(1)因为曲线y=f(x)在点(a,f(a))处与直线y=b相切,
所以f′(a)=a(2+cos a)=0,b=f(a),解得a=0,b=f(0)=1.
(2)令f′(x)=0,得x=0.
f(x)与f′(x)的情况如下:
所以函数f(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增,f(0)=1是f(x)的最小值。
当b≤1时,曲线y=f(x)与直线y=b最多只有一个交点;
当b>1时,f(-2b)=f(2b)≥4b2-2b-1>4b-2b-1>b,
f(0)=1<b,
所以存在x1∈(-2b,0),x2∈(0,2b),使得f(x1)=f(x2)=b.
由于函数f(x)在区间(-∞,0)和(0,+∞)上均单调,所以当b>1时曲线y=f(x)与直线y=b有且仅有两个不同交点。
综上可知,如果曲线y=f(x)与直线y=b有两个不同交点,那么b的取值范围是(1,+∞)。
知识点
如图,设P为抛物线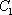
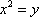
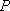
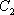
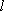
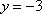
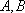
(1)求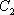
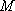
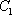
(2)是否存在点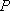
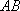
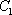
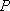
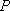
正确答案
见解析
解析
(1)解:由题意可知,抛物线C1的准线方程为:
所以圆心M到抛物线C1准线的距离为
(2)解:设点P的坐标为(x0, x02),抛物线C1在点P处的切线交直线l于点D。
再设A,B,D的横坐标分别为
过点P(x0, x02)的抛物线C1的切线方程为:
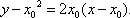
当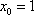
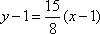
可得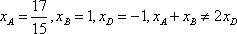
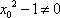
设切线PA.PB的斜率为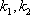
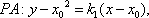
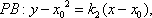
将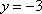
从而
又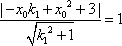
即
同理
所以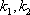
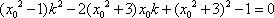
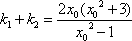
因为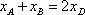
所以
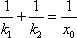
从而
进而得
综上所述,存在点P满足题意,点P的坐标为
知识点
已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(1)求a,b的值;
(2)讨论f(x)的单调性,并求f(x)的极大值。
正确答案
见解析
解析
(1)f′(x)=ex(ax+a+b)-2x-4.
由已知得f(0)=4,f′(0)=4.
故b=4,a+b=8.
从而a=4,b=4.
(2)由(1)知,f(x)=4ex(x+1)-x2-4x,
f′(x)=4ex(x+2)-2x-4=4(x+2)·
令f′(x)=0得,x=-ln 2或x=-2.
从而当x∈(-∞,-2)∪(-ln 2,+∞)时,f′(x)>0;
当x∈(-2,-ln 2)时,f′(x)<0.
故f(x)在(-∞,-2),(-ln 2,+∞)上单调递增,在(-2,-ln 2)上单调递减。
当x=-2时,函数f(x)取得极大值,极大值为f(-2)=4(1-e-2)。
知识点
已知a∈R,函数f(x)=2x3-3(a+1)x2+6ax.
(1)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若|a|>1,求f(x)在闭区间[0,2|a|]上的最小值。
正确答案
(1)y=6x-8.(2)g(a)=
解析
(1)当a=1时,f′(x)=6x2-12x+6,
所以f′(2)=6.
又因为f(2)=4,所以切线方程为y=6x-8.
(2)记g(a)为f(x)在闭区间[0,2|a|]上的最小值。
f′(x)=6x2-6(a+1)x+6a=6(x-1)(x-a)。
令f′(x)=0,得到x1=1,x2=a.
当a>1时,
比较f(0)=0和f(a)=a2(3-a)的大小可得g(a)=
当a<-1时,
得g(a)=3a-1.
综上所述,f(x)在闭区间[0,2|a|]上的最小值为g(a)=
知识点
已知函数f(x)=x2e-x.
(1)求f(x)的极小值和极大值;
(2)当曲线y=f(x)的切线l的斜率为负数时,求l在x轴上截距的取值范围。
正确答案
(1)极小值为f(0)=0;极大值为f(2)=4e-2.
(2)(-∞,0)∪[
解析
(1)f(x)的定义域为(-∞,+∞),
f′(x)=-e-xx(x-2),①
当x∈(-∞,0)或x∈(2,+∞)时,f′(x)<0;
当x∈(0,2)时,f′(x)>0.
所以f(x)在(-∞,0),(2,+∞)单调递减,在(0,2)单调递增。
故当x=0时,f(x)取得极小值,极小值为f(0)=0;
当x=2时,f(x)取得极大值,极大值为f(2)=4e-2.
(2)设切点为(t,f(t)),
则l的方程为y=f′(t)(x-t)+f(t)。
所以l在x轴上的截距为m(t)=
由已知和①得t∈(-∞,0)∪(2,+∞)。
令h(x)=

当x∈(-∞,-2)时,h(x)的取值范围是(-∞,-3)。
所以当t∈(-∞,0)∪(2,+∞)时,m(t)的取值范围是(-∞,0)∪[
综上,l在x轴上的截距的取值范围是(-∞,0)∪[
知识点
扫码查看完整答案与解析