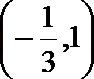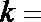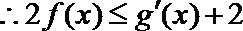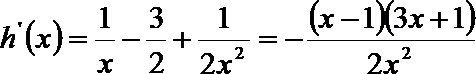- 导数的几何意义
- 共154题
21.已知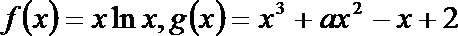
(I)如果函数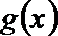
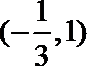
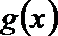
(II)在(Ⅰ)的条件下,求函数y=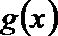
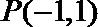
(III)若不等式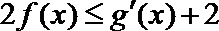
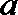
正确答案
解: (I)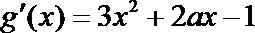
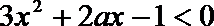
即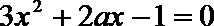
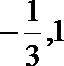
将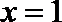
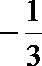
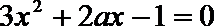
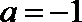
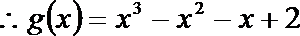
(II)由(Ⅰ)知: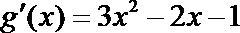
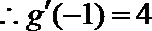
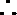
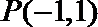
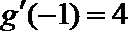
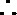
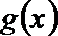
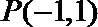
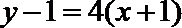
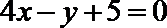
(III)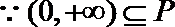
即: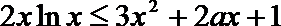
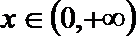
可得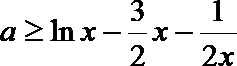
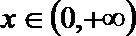
设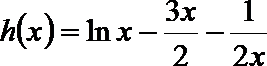
令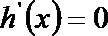
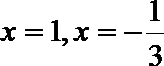
当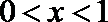
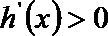
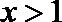
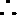
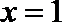
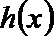
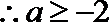
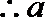
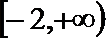
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)当

(2)设|MN|=

(3)在(2)的条件下,若对任意的正整数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若曲线
正确答案
(1,0)
解析
解析已在路上飞奔,马上就到!
知识点
16.已知曲线x在
正确答案
8
解析
y=x+lnx的导数为y′=1+1/x,曲线y=x+lnx在x=1处的切线斜率为k=2,
则曲线y=x+lnx在x=1处的切线方程为y-1=2x-2,即y=2x-1.由于切线与曲线y=ax2+(a+2)x+1相切,故y=ax2+(a+2)x+1可联立y=2x-1,得ax2+ax+2=0,又a≠0,两线相切有一切点,所以有△=a2-8a=0,解得a=8.故答案为:8.
考查方向
曲线的切线方程,导数的几何意义
解题思路
先求出曲线在切点处的切线方程,然后联立成方程组,化成一元二次方程,利用根的判别式求解。
易错点
导数的几何意义理解的不透彻,不会求切点。
知识点
扫码查看完整答案与解析