- 导数的几何意义
- 共154题
12. 已知函数

正确答案
解析
由已知的解析式可知改函数不是奇函数,所以图像不关于原点对称,排除B,C,当x<0时可知函数的导函数恒小于0 ,也就是单调递减的,所以排除D,所以选A答案。
考查方向
解题思路
根据函数的性质去做。
易错点
不会求解。
知识点
14.若曲线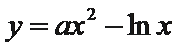
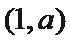
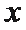
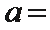
正确答案
解析
由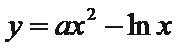
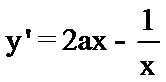
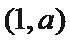
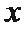
所以满足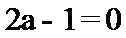

考查方向
解题思路
求导然后由导数为0求解。
易错点
不知道导数的几何意义是什么。
知识点
14、若曲线



正确答案
考查方向
解题思路
本题考查导数的几何意义——切线问题,解题步骤如下:
易错点
是在运算上出错。
知识点
5.已知实数



则使
正确答案
解析
因为



考查方向
解题思路
根据相关性质,结合选项直接选择正确答案
易错点
不理解题意,代入函数中“硬算”
知识点
19.已知函数


(1)求
(2)若对任意的


(3)若函数


正确答案
(1)
(2)
(3)
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意对参数的讨论(3)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”.涉及对数函数,要特别注意函数的定义域.
(1)由题意得


所以

(2)由(1)知

所以



又不等式整理可得

所以

当



同理,函数


综上所述,实数

(3)结论是
证明:由题意知函数

易得函数



因为



不妨令




即证

因为



综上所述,函数

考查方向
本题考查了利用导数的几何意义,利用导数求含参数的函数单调区间,分类讨论讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
本题考查导数的性质,解题步骤如下:
1、求导,然后解导数不等式,算极值。
2、对参数分类讨论求得单调区间。
3、涉及恒成立问题,转化成求函数的最值,利用“分离参数法”
易错点
1、第二问中恒成立问题,转化为求函数的最值,最值如何求解。
2、第三问中构造函数不正确得不到正确结论。
知识点
16.函数

正确答案
解析
因为







考查方向
解题思路
先求导,再利用基本不等式来求解。
易错点
导数的几何意义不清楚。
知识点
14.已知函数f(x)=ax3+x+1的图像在点(1,f(1))处的切线过点(2,7),则a= .
正确答案
1
知识点
21.已知函数


(1)设函数





(2)已知点















正确答案
(1)


解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)存在性的问题可以先假设存在然后在去求解。
(1)











故实数

(2)设


与曲线




















考查方向
解题思路
本题考查导数的性质,解题步骤如下:(1)直接按照步骤来求;(2)存在性的问题可以先假设存在然后在去求解。
易错点
第二问计算出错。
知识点
13.曲线f(x)=
正确答案
解析
考查方向
解题思路
1)对曲线函数求导,
2)求点P出的导函数值即斜率
3)使用点斜式直接写出答案
易错点
主要易错于求导出错
知识点
16.已知




正确答案
解析
当








考查方向
解题思路
由当





易错点
对函数的奇偶性、解析式、导数的几何意义理解出现错误、计算错误
知识点
扫码查看完整答案与解析



















