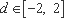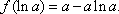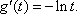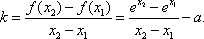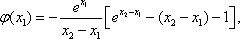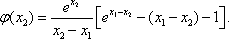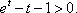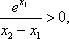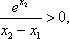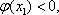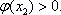- 导数的几何意义
- 共154题
设函数f(x)=axn(1-x)+b(x>0),n为正整数,a,b为常数,曲线y=f(x)在(1,f(1))处的切线方程为x+y=1.
(1)求a,b的值;
(2)求函数f(x)的最大值;
(3)证明:
正确答案
见解析
解析
(1)因为f(1)=b,由点(1,b)在x+y=1上,可得1+b=1,即b=0.
因为f′(x)=anxn-1-a(n+1)xn,所以f′(1)=-a.
又因为切线x+y=1的斜率为-1,所以-a=-1,即a=1.故a=1,b=0.
(2)由(1)知,f(x)=xn(1-x)=xn-xn+1,f′(x)=(n+1)·xn-1
令f′(x)=0,解得

在(0,
而在(
故f(x)在(0,+∞)上的最大值为
(3)令φ(t)=ln t-1+
则
在(0,1)上,φ′(t)<0,
故φ(t)单调递减;
而在(1,+∞)上,φ′(t)>0,
故φ(t)单调递增,
故φ(t)在(0,+∞)上的最小值为φ(1)=0,
所以φ(t)>0(t>1),
即ln t>1-
令t=1+

即
所以

由(2)知,
故所证不等式成立。
知识点
已知P,Q为抛物线x2=2y上两点,点P,Q的横坐标分别为4,-2,过P,Q分别作抛物线的切线,两切线交于点A,则点A的纵坐标为( )
正确答案
解析
如图所示,由已知可设
P(4,y1),Q(-2,y2),
∵点P,Q在抛物线x2=2y上,
∴
∴
∴P(4,8),Q(-2,2),又∵抛物线可化为
∴过点P的切线斜率为
∴过点P的切线为y-8=4(x-4),即
y=4x-8。
又∵过点Q的切线斜率为
∴过点Q的切线为y-2=-2(x+2),即y=-2x-2。
联立
∴点A的纵坐标为-4
知识点
已知函数


(1)若曲线



(2)求函数
(3)当



正确答案
见解析
解析
本小题主要考查函数与导数,函数的单调性、极值、零点等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、数形结合思想、分类与整合思想、化归与转化思想,满分14分。
(1)由

又曲线


得


(2)
①当




②当







所以


故


综上,当

当



(3)当
令
则直线


等价于方程

假设


又函数





又



所以

解法二:
(1)(2)同解法一。
(3)当

直线


等价于关于




在
①当


②当

令

令

当

当





从而

所以当
解得

综上,得

知识点
若函数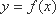

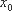
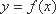
已知

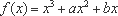
(1)求

(2)设函数
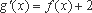
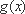
(3)设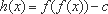
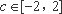
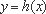
正确答案
(1)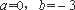
解析
(1)由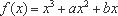
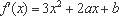
∵1和
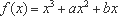
∴ 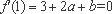
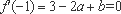
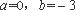
(2)∵ 由(1)得,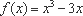
∴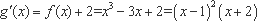
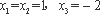
∵当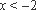
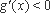
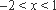
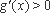
∴
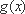
∵当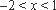
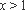
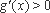
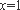
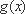
∴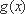
(3)令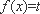
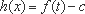
先讨论关于
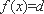
当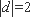
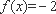
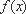
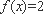
当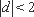
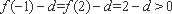
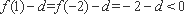
∴一2 , -1,1 ,2 都不是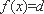
由(1)知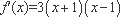
① 当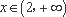
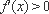
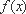
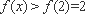
此时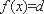
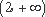
② 当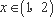
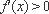
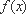
又∵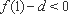
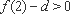
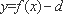
∴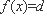
同理,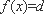
③ 当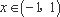
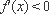
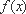
又∵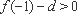
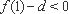
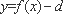
∴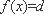
因此,当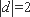
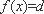


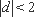
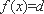
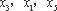
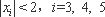
现考虑函数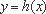
( i )当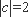
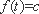

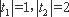
而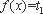
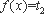
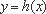
( 11 )当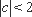
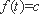
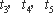
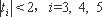
而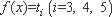
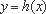
综上所述,当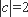
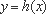
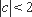
知识点
已知函数f(x)=ex-ax,其中a>0.
(1)若对一切x∈R,f(x) 
(2)在函数f(x)的图像上去定点A(x1, f(x1)),B(x2, f(x2))(x1<x2),记直线AB的斜率为k,证明:存在x0∈(x1,x2),使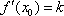
正确答案
见解析
解析
解: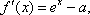
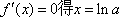
当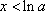
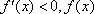
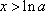
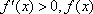
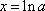
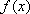
于是对一切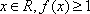
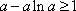
令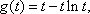
当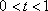
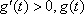
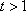
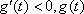
故当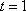
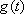
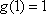
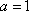
综上所述,
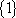
(2)由题意知,
令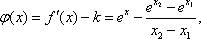
令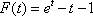
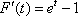
当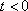
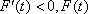
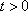
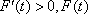
故当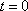
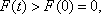
从而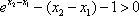
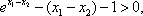
所以
因为函数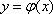
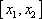
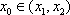
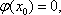
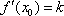
知识点
扫码查看完整答案与解析