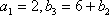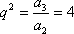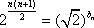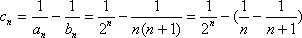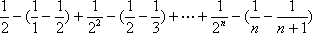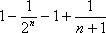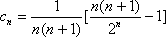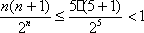- 分组转化法求和
- 共36题
1
题型:简答题
|
已知数列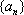
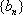
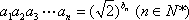
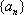
(1) 求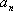
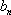
(2) 设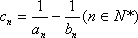


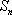
(i)求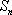
(ii)求正整数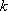
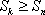
正确答案
见解析
解析
(1)∵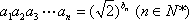
当n≥2,n∈N*时,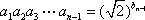
由①②知:当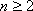
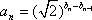
∵b3=6+b2, ∴a3=8。
∵{an}为等比数列,且a1=2,∴{an}的公比为q,则
由题意知an>0,∴q>0,∴q=2。
∴an=2n(n∈N*)。
又由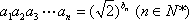
即
∴bn=n(n+1)(n∈N*)。
(2)(i)∵
∴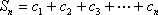
=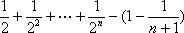
=
(ii)因为c1=0,c2>0,c3>0,c4>0;
当n≥5时,
而
所以,当n≥5时,cn<0,
综上,对任意n∈N*恒有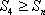
知识点
由递推关系式求数列的通项公式等比数列的性质及应用分组转化法求和数列与不等式的综合
1
题型:简答题
|
已知数列


(1)求
(2)求

(3)记数列




正确答案
(1)3,13,39(2)
解析
(1)


(2)由题知,有

∴
(3) ∵
∴
∴
又






综上,有
知识点
由递推关系式求数列的通项公式分组转化法求和
1
题型:填空题
|
已知数列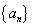

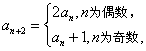

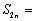
正确答案
7;
解析
略
知识点
由递推关系式求数列的通项公式分组转化法求和
1
题型:
单选题
|
定义在R上的函数f(x)满足f(x+6)=f(x),当-3≤x<-1时,f(x)=-(x+2)2,当-1≤x<3时,f(x)=x。则f(1)+f(2)+f(3)+…+f(2012)=
正确答案
B
解析


知识点
函数的周期性分组转化法求和
1
题型:简答题
|
在公差为



(1)求
(2)若
正确答案
(1)
(2)
解析
(1)由已知得到:


(2)由(1)知,当

①当
②当
所以,综上所述:
知识点
分组转化法求和等差数列与等比数列的综合
下一知识点 : 错位相减法求和
扫码查看完整答案与解析