- 直线与椭圆的位置关系
- 共59题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知数列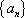

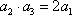
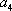
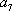

正确答案
解析
设{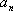
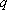
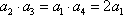
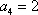
由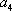
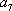

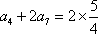

∴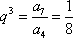
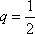
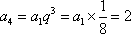
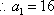
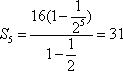
知识点
正确答案
(1) C的离心率为
(2)
解析
知识点
已知函数

证明:(1)存在唯一

(2)存在唯一


正确答案
见解析
解析
(1)∵当x∈(0,

∴函数f(x)在(0,
又f(0)=π﹣


∴存在唯一的x0∈(0,
(2)考虑函数h(x)=


令t=π﹣x,则x∈[

记u(t)=h(π﹣t)=

则u′(t)=
由(1)得,当t∈(0,x0)时,u′(t)<0;
在(0,x0)上u(x)是增函数,又u(0)=0,∴当t∈(,x0]时,u(t)>0,
∴u(t)在(0,x0]上无零点;
在(x0,

∴存在唯一的t1∈(x0,
∴存在唯一的t1∈(0,
∴存在唯一的x1=π﹣t1∈(
∵当x∈(
∴存在唯一的x1∈(
∵x1=π﹣t1,t1>x0,∴x0+x1<π。
知识点
若曲线


正确答案
解析
曲线







知识点
扫码查看完整答案与解析