直线与椭圆的位置关系
共59题

· 直线与椭圆的位置关系

直线与椭圆的位置关系
共59题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知椭圆过右焦点F且斜率为k（k＞0）的直线于C相交于A、B两点，若则k=（　　）

正确答案

解析

知识点

向量在几何中的应用椭圆的几何性质直线与椭圆的位置关系

题型：简答题

简答题 · 14 分

已知椭圆的四个顶点恰好是一边长为2，一内角为的菱形的四个顶点。

（1）求椭圆的方程；

（2）直线与椭圆交于，两点，且线段的垂直平分线经过点，求（为原点）面积的最大值。

正确答案

（1）

（2）

解析

（1）因为椭圆的四个顶点恰好是一边长为2，

一内角为的菱形的四个顶点,

所以,椭圆的方程为 …………………4分

（2）设因为的垂直平分线通过点，显然直线有斜率，

当直线的斜率为时,则的垂直平分线为轴,则

所以

因为，

所以，当且仅当时，取得最大值为 ………………6分

当直线的斜率不为时,则设的方程为

所以，代入得到

当, 即

方程有两个不同的解

又， …………………9分

所以，又，化简得到

代入，得到 …………………10分

又原点到直线的距离为

所以

化简得到 …………………12分

因为，所以当时，即时，取得最大值

综上，面积的最大值为 …………………14分

知识点

椭圆的定义及标准方程直线与椭圆的位置关系圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 14 分

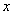
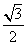
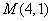
已知椭圆的中心在原点，焦点在轴上，离心率为，且经过点.

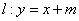
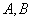
直线交椭圆于两不同的点.

（1）求椭圆的方程；

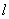
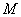
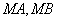
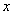
（2）若直线不过点,求证：直线与轴围成等腰三角形.

正确答案

见解析。

解析

知识点

椭圆的定义及标准方程直线与椭圆的位置关系直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 14 分

已知椭圆的右焦点为，短轴的端点分别为，且

（1）求椭圆的方程；

（2）过点且斜率为的直线交椭圆于两点，弦的垂直平分线与轴相交于点.设弦的中点为，试求的取值范围。

正确答案

（1）

（2）

解析

（1）依题意不妨设，，则，.

由，得.又因为，

解得.

所以椭圆的方程为. ……………4分

（2）依题直线的方程为.

由得.

设，，则，. …………6分

所以弦的中点为. ……………7分

所以

. ……………9分

直线的方程为，

由，得，则，

所以. …………11分

所以.……………12分

又因为，所以.

所以.

所以的取值范围是. ……………………14分

知识点

椭圆的定义及标准方程直线与椭圆的位置关系圆锥曲线中的范围、最值问题直线、圆及圆锥曲线的交汇问题

题型：简答题

简答题 · 14 分

已知：椭圆（），过点，的直线倾斜角为，原点到该直线的距离为。

（1）求椭圆的方程；

（2）斜率大于零的直线过与椭圆交于，两点，若，求直线的方程；

（3）是否存在实数，直线交椭圆于，两点，以为直径的圆过点？若存在，求出的值；若不存在，请说明理由。

正确答案

见解析

解析

（1）由，，得，，

所以椭圆方程是：-----------------4分

（2）设EF：（）代入，得，

设，，由，得。

由，--------------6分

得，，（舍去），（没舍去扣1分）

直线的方程为：即--------------------9分

（3）将代入，得（*）

记，，PQ为直径的圆过，则，即，又，，得。

解得，此时（*）方程，

存在，满足题设条件。-----------------14分

知识点

椭圆的定义及标准方程直线与椭圆的位置关系圆锥曲线的定点、定值问题圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

继续学习学习下一知识点

下一知识点 : 直线与双曲线的位置关系

百度题库 > 高考 > 理科数学 > 直线与椭圆的位置关系

扫码查看完整答案与解析