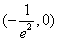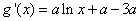- 导数的乘法与除法法则
- 共1249题
把边长为



正确答案
解析
略
知识点
已知函数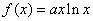
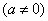
(1)求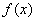
(2)当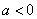
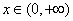
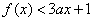
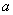
正确答案
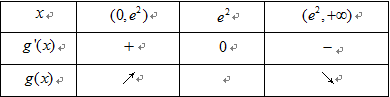
(1)函数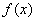
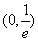
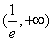
(2)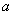
解析
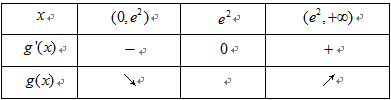
(1)函数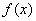
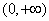
因为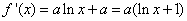
令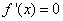
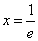
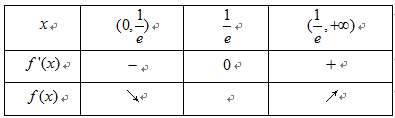
① 当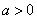
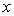
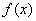
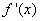
即函数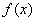
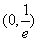
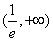
② 当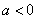
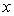
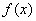
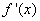
即函数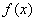
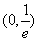
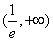
(2)当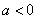
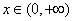
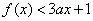
即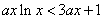
所以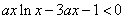
设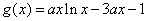
因为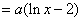
令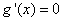
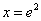
因为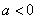
所以随着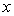
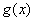
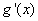
即函数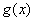
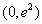
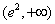
所以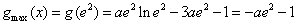
所以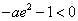
所以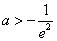
所以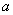
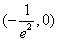
法二:
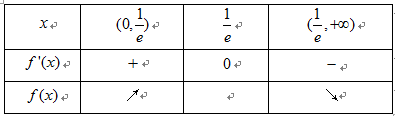
当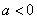
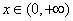
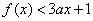
即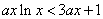
所以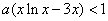
即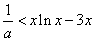
设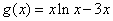
因为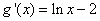
令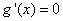
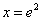
所以随着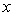
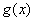
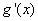
即函数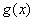
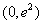
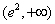
所以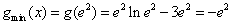
所以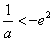
所以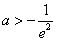
所以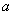
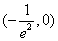
知识点
已知

①


②

则m的取值范围是_______。
正确答案
解析
根据


































知识点
已知函数
(1)求
(2)求
正确答案
见解析
解析
知识点
数列









(1)求

(2)求数列

(3)证明:对一切正整数

正确答案
见解析。
解析
(1)由

由

(2)因为



因为



因为数列


于是当

将②、③代入①式,可得
因此数列
(注:学生不写上述陈述扣1分)
所以

由③式,可得当

当



(3)由(2)可知,所证明的不等式为
方法一:首先证明

因为

所以当

当

综上所述,对一切正整数
方法二:
当

当



(验证不写扣1分)
综上所述,对一切正整数
方法三:
当


当



当

(验证不写扣1分)
综上所述,对一切正整数

知识点
扫码查看完整答案与解析