导数的乘法与除法法则
共1249题

· 导数的乘法与除法法则

导数的乘法与除法法则
共1249题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

某工厂生产甲，乙两种芯片，其质量按测试指标划分为：指标大于或等于82为合格品，小于82为次品.现随机抽取这两种芯片各100件进行检测，检测结果统计如下：

（1）试分别估计芯片甲，芯片乙为合格品的概率；

（2）生产一件芯片甲，若是合格品可盈利40元，若是次品则亏损5元；生产一件芯片乙，若是合格品可盈利50元，若是次品则亏损10元.在（1）的前提下，

（a）记X为生产1件芯片甲和1件芯片乙所得的总利润，求随机变量X的分布列和数学期望；

（b）求生产5件芯片乙所获得的利润不少于140元的概率.

正确答案

见解析。

解析

（1）芯片甲为合格品的概率约为,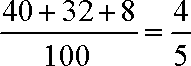

芯片乙为合格品的概率约为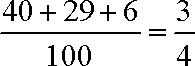。 ………………3分

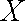
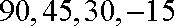
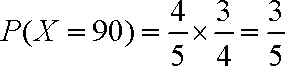
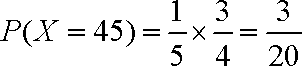
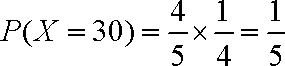
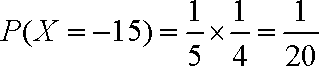
（2）（ⅰ）随机变量的所有取值为。

；；

；。

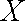
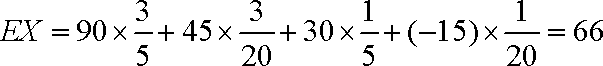
所以，随机变量的分布列为:

。 ………………8分

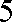
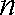
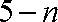
（ⅱ）设生产的件芯片乙中合格品有件，则次品有件.

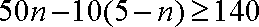
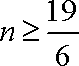
依题意，得，解得，

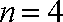
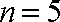
所以，或，

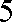
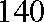
设“生产件芯片乙所获得的利润不少于元”为事件，

则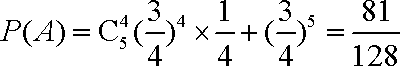， ………………12分

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 10 分

设ξ为随机变量，从棱长为1的正方体ABCD﹣A1B1C1D1的八个顶点中任取四个点，当四点共面时，ξ=0，当四点不共面时，ξ的值为四点组成的四面体的体积。

（1）求概率P（ξ=0）；

（2）求ξ的分布列，并求其数学期望E（ξ）。

正确答案

见解析。

解析

（1）从棱长为1的正方体ABCD﹣A1B1C1D1的八个顶点中任取四个点，共有=70种情况，当四点共面时，共有12种情况，

∴P（ξ=0）==。

（2）四点不共面时，四面体的体积有以下两种情况：

①四点在相对面且异面的对角线上，体积为1﹣4×=，这样的取法共有2种；

②四点中有三个点在一个侧面上，另一个点在相对侧面上，体积为，这样的取法共有70﹣12﹣2=56种。

∴ξ的分布列为

数学期望E（ξ）=。

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 12 分

如图, 已知单位圆上有四点, 分别的面积为.

（1）用表示；

（2）求的最大值及取最大值时的值。

正确答案

（1），（2）

解析

解析：（1）根据三角函数的定义, 知

所以, 所

.----------3分

又因为四边形OABC的面积＝

所以.---------------6分

（2）由（1）知.-----------9分

因为, 所以, 所以,

所以的最大值为, 此时的值为. -------------12分

知识点

导数的乘法与除法法则

题型：单选题

单选题 · 5 分

已知函数f(x)=-2lnx(a∈R)，g(x)=，若至少存在一个x0∈[1，e]，使得f(x0)>g(x0)成立，则实数a的范围为

A[1，+∞)

B(1，+∞)

C[0，+∞)

D(0，+∞)

正确答案

解析

设h(x)=f(x)-g(x)=ax-2lnx，则.若a≤0，则h′(x)<0，h(x)是减函数，在[1，e]上的最大值为h(1)=a≤0，∴不存在x0∈[1，e]，使得h(x0)>0，即f(x0)>g(x0)成立；若a>0，则由h(1)=a>0知，总存在x0=1使得f(x0)>g(x0)成立。故实数a的范围为(0，+∞).

知识点

导数的乘法与除法法则

题型：简答题

简答题 · 12 分

在⊿ABC中，角A、B、C所对的边分别为a、b、c，且cos2C=cosC.

（1）求角C；

（2）若b=2a，⊿ABC的而积S=sinA·sinB，求sinA及边c的值。

正确答案

见解析

解析

（1）∵cos2C=cosC，∴2cos2C-cosC-1=0

即(2cosC+1)(cosC-1)=0，又0<C<π，∴，∴C=.………6′

（2）由余弦定理得：c2=a2+(2a)2-2a·(2a)cos=7a2，∴c=a

又由正弦定理得：sinC=sinA，∴sinA=.………9′

∵S=absinC，∴absinC=sinA·sinB，

∴，得：c=sin=.………12′

知识点

导数的乘法与除法法则

继续学习学习下一知识点

下一知识点 : 简单复合函数的导数

百度题库 > 高考 > 理科数学 > 导数的乘法与除法法则

扫码查看完整答案与解析