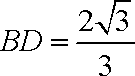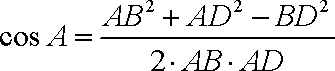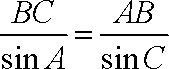- 导数的乘法与除法法则
- 共1249题
已知二阶矩阵M有特征值



正确答案
见解析。
解析
设

再由
联立以上方程组解得a=2,b=1,c=0,d=1,故
知识点
要得到函数

正确答案
解析
将


知识点
已知:
求证:
正确答案
见解析。
解析
因为|m|+|n|≥|m-n|,
所以
又

所以
知识点
在△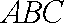

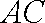
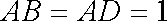
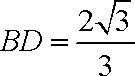
(1)求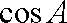
(2)求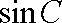
正确答案
见解析
解析
(1)在△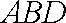
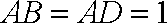
∴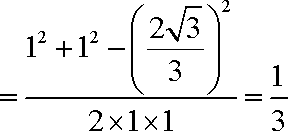
(2)由(1)知,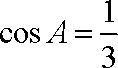

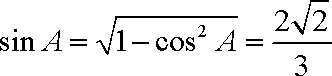
∵
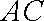

在△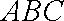
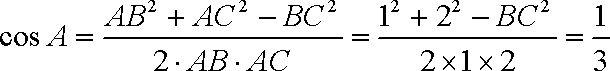
解得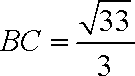
∴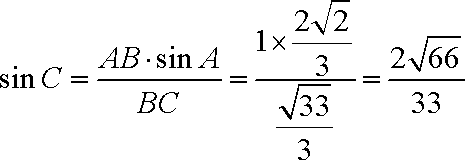
知识点
已知函数

(1)求
(2)若
(ⅰ)求实数
(ⅱ)已知数列






正确答案
见解析
解析
(1)函数


当



当




所以


综上述:






(2)(ⅰ)由(1)知,当

当

令

由



所以


故

因此,
(ⅱ)因为

由




猜想当


下面用数学归纳法进行证明。
①当


②假设当








所以


故

根据①②可知,当


因此,

知识点
扫码查看完整答案与解析