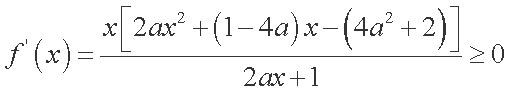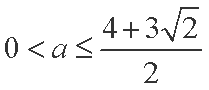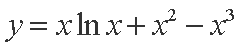- 导数的乘法与除法法则
- 共1249题
如图,在直三棱柱ABC-A1B1C1中,∠ BAC=90°,AB=AC=AA1 =1。D是棱CC1上的一点, P是AD的延长线与A1C1的延长线的交点,且

(1)求证:CD=C1D
(2)求二面角A-A1D-B的平面角的余弦值;
(3)求点C到平面B1DP的距离
正确答案
见解析
解析
(1)连接










(2)由题意


则


在

则
(3)因为


在


知识点
已知


(1)求函数

(2)是否存在实数




(3)求证:
正确答案
见解析
解析
(1)函数
∵ 

① 若




② 若




∴


∴当


③ 若



∴当


综上:
(2) ∵ 
由(1)可知:当


∴

∵曲线



而 

故不存在实数



(3)由(1)可知:当


即 当

取
∴
故
又 在(*)式中,取
∴
故
或:又 在(*)式中,取
得:
∴
故
知识点
已知函数f(x)=1n(2ax+1)+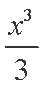
(1)若y=f(x)在[4,+∞)上为增函数,求实数a的取值范围;
(2)当a=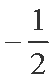
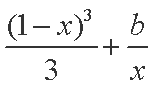
正确答案
(1)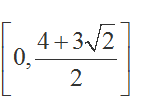
解析
解析:
(1)因为函数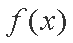
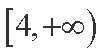
在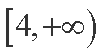
①当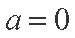
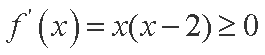
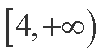
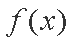
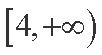
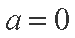
②当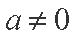
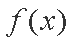
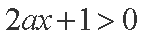
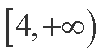
故只能
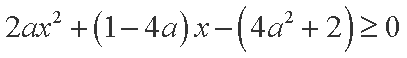
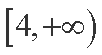
令函数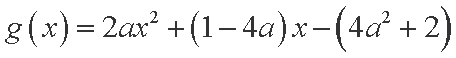
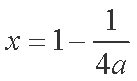

所以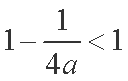
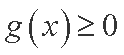
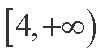
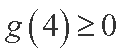
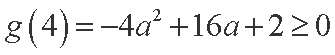
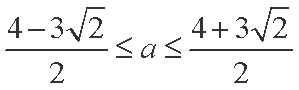

综上所述,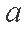
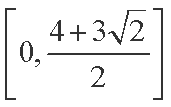

(2)当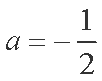
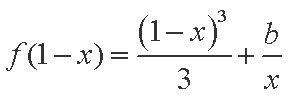
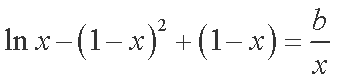
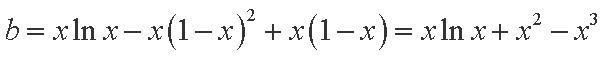
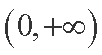

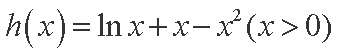
则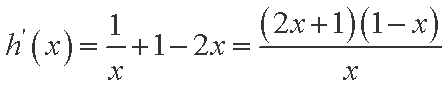
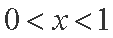
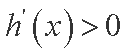
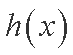
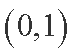
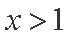
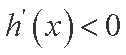
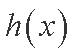
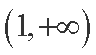
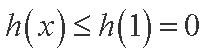

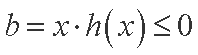
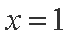
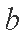


知识点
某人2002年底花100万元买了一套住房,其中首付30万元,70万元采用商业贷款,贷款的月利率为5‰,按复利计算,每月等额还贷一次,10年还清,并从贷款后的次月开始还贷。
(1)这个人每月应还贷多少元?
(2)为了抑制高房价,国家出台“国五条”,要求卖房时按照差额的20%缴税,如果这个人现在将住房150万元卖出,并且差额税由卖房人承担,问:卖房人将获利约多少元?(参考数据:(1+0.005)120≈1.8)
正确答案
见解析
解析
(1)设每月应还贷x元,共付款12×10=120次,则有
x[1+(1+0.005)+(1+0.005)2+…+(1+0.005)119]=700000(1+0.005)120,
所以
则
答:每月应还贷7875元。
(2)卖房人共付给银行7875×120=945000元,
利息945000﹣700000=245000(元),
缴纳差额税(1500000﹣1000000)×0.2=100000(元),
获利500000﹣(245000+100000)=155000(元)。
答:卖房人将获利约155000元。
知识点
甲、乙、丙三人投篮, 甲的命中率为


(1) 当

(2) 当



正确答案
见解析
解析
解:(1)当



(2)




所以






知识点
扫码查看完整答案与解析