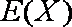- 导数的乘法与除法法则
- 共1249题
已知二次函数




(1)求
(2)求阴影面积S关于t的函数S(t)的解析式;
正确答案
见解析。
解析
(1)由图形可知二次函数的图象过点(0,0),(8,0),并且f(x)的最大值为16
则
∴函数f(x)的解析式为
(2)由
∵0≤t≤2,∴直线l1与f(x)的图象的交点坐标为(
由定积分的几何意义知:
知识点
如图,在正三棱柱







(1)求异面直线

(2)求二面角
正确答案
见解析。
解析
(1)以












所以

所以
所以异面直线


(2)平面

设平面



由



所以
所以二面角

知识点
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
(1)试分别估计元件A、元件B为正品的概率;
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望。
正确答案
见解析
解析
(1)由题可知 元件A为正品的概率为 

(2)(i)设生产的5件元件中正品件数为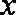
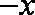
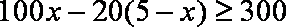
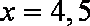
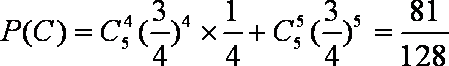
(ii)随机变量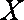
则
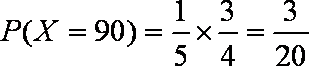
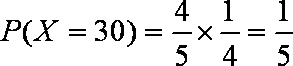
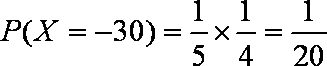
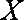

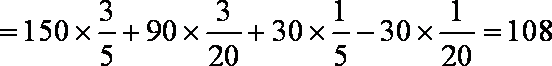
知识点
设函数

(1)若函数


(2)求函数
(3)设








正确答案
见解析
解析
(1)
依题意得,在区间

又因为


所以实数

(2)
①显然,当




②当
(ⅰ)当





(ⅱ)当

易知,当


当



所以,当




综上,当

当




(3)由已知得
得:
由

=
令




知识点
已知数列{an}满足a1=2,
(1)证明:an>n(n≥3);
(2)证明:
正确答案
见解析。
解析
(1)①因为a1=2,a2=2,所以
②假设n=k(k≥3)时不等式成立,即ak>k(k≥3);
那么,当n=k+1时,因为
所以,
由①②数学归纳法知,当n≥3时an>n,
(2)由(1)知,

所以


所以

知识点
扫码查看完整答案与解析