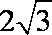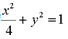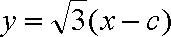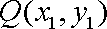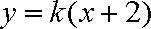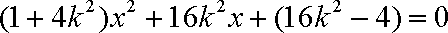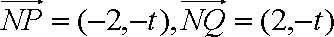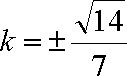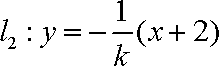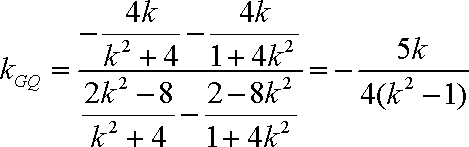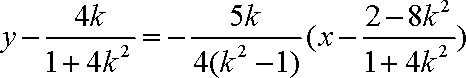- 导数的乘法与除法法则
- 共1249题
如题是收集重庆市2013年的9月和气象才几点处的平均气温,(单位:
正确答案
解析
解析:由图可知,平均气温在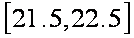
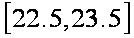
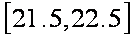
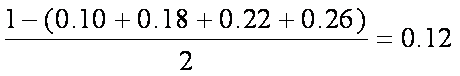
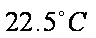
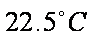
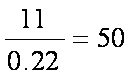
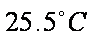
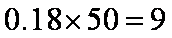
故选:D
知识点
已知




(1)求角
(2)若向量

正确答案
(1)
解析
解析:(1)由题意得
即
由余弦定理得

(2)


所以

知识点
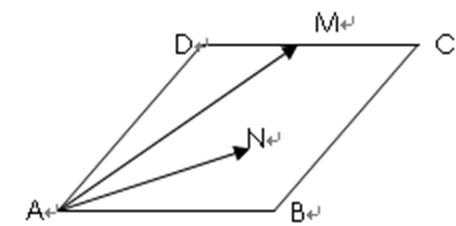
如图,菱形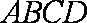
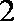
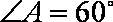
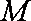
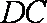
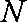
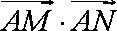
正确答案
解析
以A点为坐标原点,建立直角坐标系,因为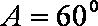
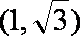
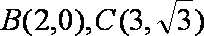
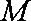
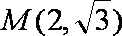
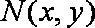
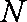
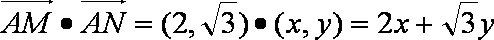
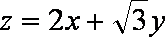
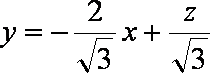
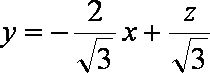
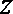
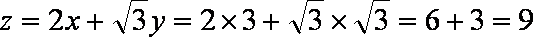
知识点
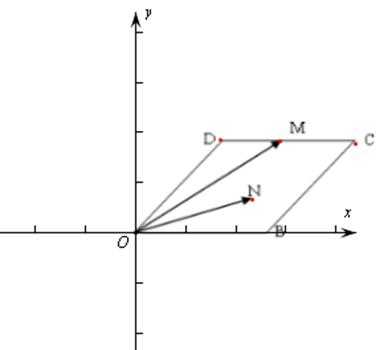
设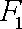
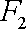

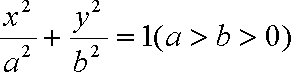
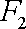


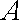
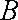
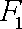
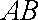


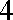
(1)求椭圆
(2)过椭圆
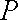
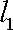

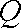
(ⅰ)若点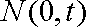

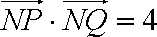
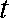
(ⅱ)过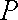
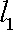
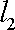


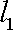
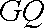

正确答案
(1)
(2)(ⅰ)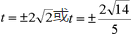
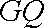

解析
解析:(1)设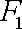
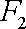
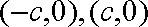
由题意得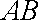
因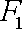
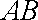

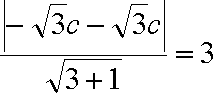
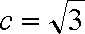
所以有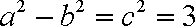
由题意知: 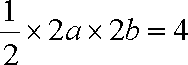
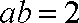
联立①②解得:
所求椭圆
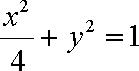
(2)由(1)知: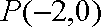
根据题意可知直线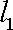
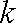
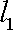
把它代入椭圆
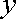
由韦达定理得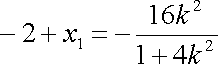
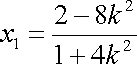
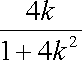
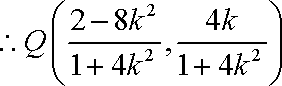

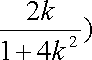
(ⅰ)当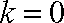
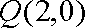

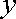
于是
由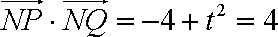
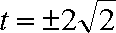
当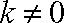

因为点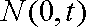

令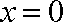
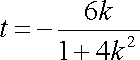
由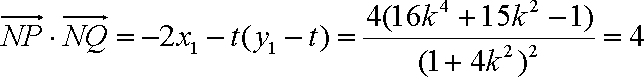
代入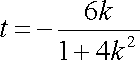
综上, 满足条件的实数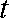
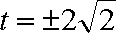
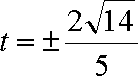
(ⅱ)设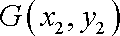
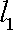
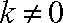
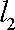
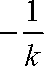
由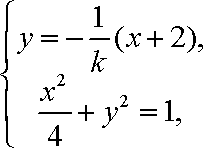
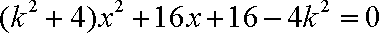
∵此方程有一根为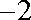
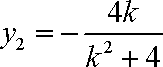
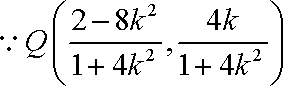
所以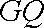
令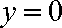
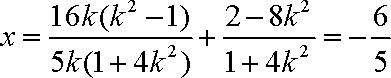
所以直线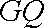

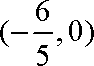
知识点
阅读右侧程序框图,则输出的数据
正确答案
0
解析
第一次运算,





知识点
扫码查看完整答案与解析