- 导数的乘法与除法法则
- 共1249题
已知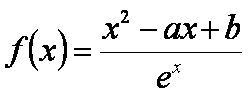
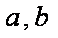
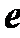
(1)若曲线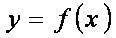
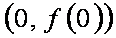

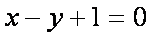
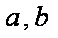
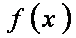
(2)已知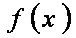
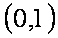
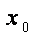
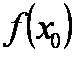
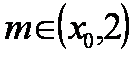
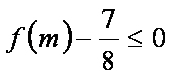
正确答案
见解析
解析
(1)f ′ (x)=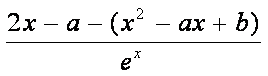
因f (x)在点(0, f (0))处的切线方程为x-y+1=0,有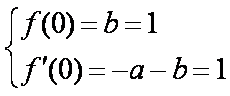
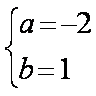
所以f ′ (x)=-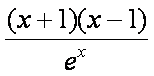
同理,f (x
(2)由f (x)在区间 (0,1) 上有且仅有一个极值点x0,且f (x0)为极大值,可知

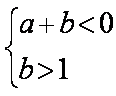
而f (2)=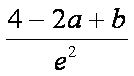
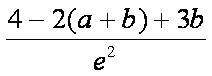
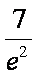
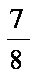
由f (x)在(x0, 2)上单调递减,则对
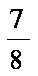
故不存在m∈(x0, 2),使f (m)-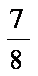
知识点
已知i是虚数单位,则
正确答案
解析
解:

知识点
直线

正确答案
解析
根据题意画出图形,如图所示:
在Rt△AOB中,由|OA|=2,|OB|=2
根据勾股定理得:|AB|=
∵OA=
∴∠BAO=60°,又OA=OC,
∴△AOC为等边三角形,
∴∠AOC=60°,又圆O的半径OA=2,
∴



故答案为:
知识点
已知抛物线y=ax2(a∈R)的准线方程为y=﹣1,则a= _________ 。
正确答案
解析
抛物线y=ax2的标准方程为 x2=





知识点
设正项数列




(1)求
(2)求证:
正确答案
见解析
解析
(1)由




相减有

又n=2时,





则有an+1-an=1(n≥1),且a1=

(2)由(1),Sn=



令f (x)=x-ln(1+x) (x


故f (x)在(0,+∞)单调递增,f (x)>f (0)=0,所以ln(1+x)<x (x>0),
故ln bn+1=ln bn+





ln bn+1-ln bn<



故ln bn+1 =(ln bn+1-ln bn)+(ln bn-ln bn-1)+…+(ln b2-ln b1)
<










=









即ln bn+1<

当n=1时,b1<e2,故bn<e2。
知识点
扫码查看完整答案与解析