正弦定理的应用
共22题

· 正弦定理的应用

正弦定理的应用
共22题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

16．给出下列四个命题：

①设，则的充要条件是且；

②任意的锐角三角形中，有成立；

③平面上n个圆最多将平面分成个部分；

④空间中直角在一个平面上的正投影可以是钝角。

其中真命题的序号是（）（要求写出所有真命题的序号）。

正确答案

②④

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定命题的真假判断与应用正弦定理的应用平行投影及平行投影作图法

题型：简答题

简答题 · 12 分

18．已知的内角A、B、C所对的边为， , ，且与所成角为．

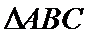
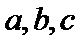
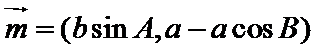
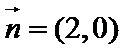
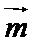
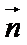
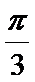
（Ⅰ）求角B的大小；

（Ⅱ）求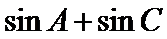的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用两角和与差的正弦函数正弦定理的应用平面向量数量积的运算

题型：简答题

简答题 · 12 分

16.已知ABC中,角A,B,C的对边分别为a,b,c, 若向量与向量共线.

（1）求角C的大小;

（2）若,求a, b的值。

正确答案

（1）C=

（2）a=2,b=4或a=4,b=2

解析

解析已在路上飞奔，马上就到！

知识点

正弦定理的应用余弦定理的应用平面向量共线（平行）的坐标表示

题型：简答题

简答题 · 12 分

17．在中，角的对边分别为,已知；

（Ⅰ）求证：成等差数列；

（Ⅱ）若的面积为，求.

正确答案

见解析

解析

（Ⅰ）

证明：由正弦定理得：

即

成等差数列.

（Ⅱ）

得

考查方向

解三角形、等差数列

解题思路

第一问根据正弦定理得到三个角的正弦关系，进而建立角与边的关系，第二问利用正弦定理求面积公式求解

易错点

正弦定理误用、化简整理错误

知识点

三角函数中的恒等变换应用二倍角的余弦正弦定理的应用等差数列的判断与证明

题型：填空题

填空题 · 5 分

在中，若,，，则=（）

正确答案

解析

略

知识点

正弦定理的应用

题型：简答题

简答题 · 12 分

在ABC中，内角A，B，C的对边分别为a，b，c.已知.

（1）求的值；

（2）若cosB=，

正确答案

（1）=2

（2）b=2

解析

(1)由正弦定理得所以=,即,即有,即,所以=2.

(2)由(1)知=2,所以有,即c=2a,又因为的周长为5,所以b=5-3a,由余弦定理得：

，即，解得a=1，所以b=2.

知识点

正弦定理的应用余弦定理

题型：填空题

填空题 · 4 分

在中，若，则。

正确答案

。

解析

由正弦定理得又所以。

知识点

正弦定理的应用

题型：简答题

简答题 · 12 分

在中，角所对的边分别为且满足

（1）求角的大小；

（2）求的最大值，并求取得最大值时角的大小。

正确答案

（1）（2）

解析

（1）由正弦定理得

因为所以

（2）由（I）知于是

取最大值2。

综上所述，的最大值为2，此时

知识点

三角函数的恒等变换及化简求值正弦定理的应用

题型：单选题

单选题 · 5 分

在△ABC中，∠A＝，AB＝2，且△ABC的面积为，则边AC的长为

正确答案

解析

略

知识点

正弦定理的应用

题型：填空题

填空题 · 5 分

在锐角△ABC中，若C=2B，则的范围是　_________　。

正确答案

解析

因为锐角△ABC中，若C=2B所以A=180°﹣B

∴

∴30°＜B＜45°

由正弦定理可得，

∵

∴

知识点

正弦定理的应用

继续学习学习下一知识点

下一知识点 : 余弦定理

百度题库 > 高考 > 文科数学 > 正弦定理的应用

扫码查看完整答案与解析