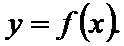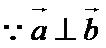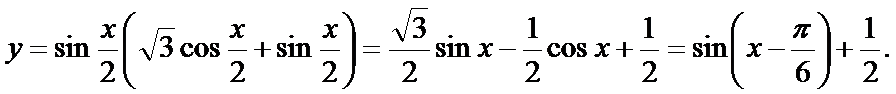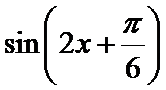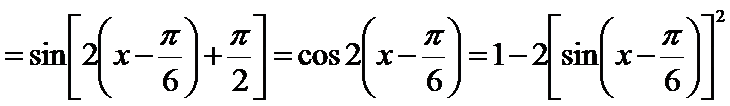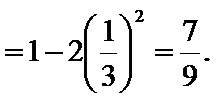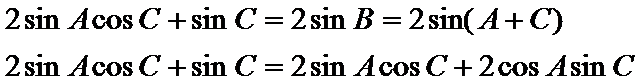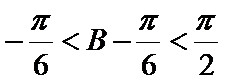- 正弦定理的应用
- 共22题
在△ABC中,角A,B,C所对的边分别是a,b,c,且
(I)证明:sinAsinB=sinC;
(II)若
正确答案
(Ⅰ)根据正弦定理,可设
则a=ksin A,b=ksin B,c=ksinC.
代入

sin A sin B=sin Acos B=sin (A+B).
在△ABC中,由A+B+C=π,有sin (A+B)=sin (π–C)=sin C,
所以sin A sin B=sin C.
(Ⅱ)由已知,b2+c2–a2=

所以sin A=
由(Ⅰ),sin Asin B=sin Acos B +cos Asin B,
所以


故tan B=
知识点
9.在△ABC中 ,B=
正确答案
知识点
15.△ABC的内角A,B,C的对边分别为a,b,c,若

正确答案
知识点
18.
在△ABC中,角A,B,C所对的边分别是a,b,c,且
(I)证明:sinAsinB=sinC;
(II)若
正确答案
知识点
已知函数
17.当

18.若




正确答案
(1)
解析
(1)



考查方向
解题思路
1。第(1)问先化简函数为一个角的一个三角函数,然后求其值域;
易错点
1.第(1)问直接将区间的端点带入函数导致值域出错;
正确答案
(2)
解析
(2)∵由题意可得

化简可得:





考查方向
解题思路
2.先由


易错点
2.第(2)问
13.设


正确答案
4
解析
由





正弦定理与余弦定理.
考查方向
解题思路
本题考查正弦定理与余弦定理的应用,先由正弦定理将
易错点
注意运算的准确性及最后结果还需开方.
知识点
已知向量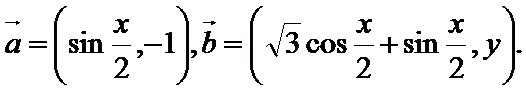
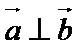
17.若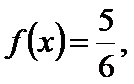
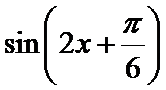
18.在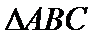
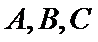
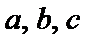
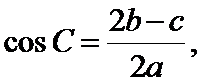
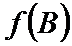
正确答案
解析
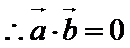
得
即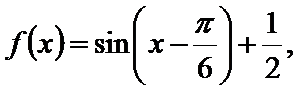
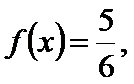
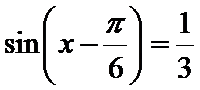
考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-
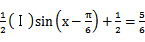
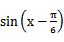

易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由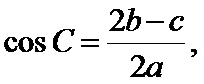
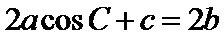
∴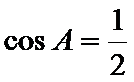

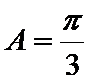
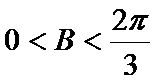
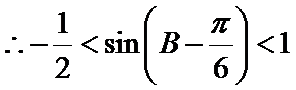
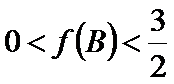
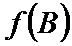
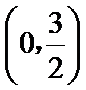
考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
已知向量

17.若

18.在




正确答案
解析

得
即


考查方向
解题思路
先通过向量垂直,得到三角关系,利用辅助角公式得到三角函数的解析式y=sin(x-



易错点
向量的坐标运算,三角函数的恒等变换
正确答案
(0,
解析
由

∴







考查方向
解题思路
将边用正弦定理进行转化,得到cosA=


易错点
向量的坐标运算,三角函数的恒等变换
5.在



正确答案
解析
因为
所以,


故选:C
考查方向
解题思路
由条件利用正弦定理化简
易错点
本题在利用正弦定理化简
知识点
17.在△ABC中,B=

正确答案
△ABC是等边三角形.
解析
试题分析:本题属于解三角形的基本问题,(1)直接按照已知条件转换成关于角C有关的表达式,最后将式子化简后来求.
在△ABC中,根据
得
同理BC=2sinA,因此AB+BC=2sinC+2sinA
因此AB+BC的最大值为

考查方向
解题思路
本题考查正弦定理和三角函数,解题步骤如下:1、根据正弦定理将边转化为只与角C有关的式子,然后用化简后用辅助角公式合二为一,最后求出最大值及取到最大值的角C,从而判断出此时三角形的形状。
易错点
利用辅助角公式进行合二为一。
知识点
扫码查看完整答案与解析