- 正弦定理的应用
- 共22题
1
题型:填空题
|
16.给出下列四个命题:
①设



②任意的锐角三角形

③平面上n个圆最多将平面分成
④空间中直角在一个平面上的正投影可以是钝角。
其中真命题的序号是( )(要求写出所有真命题的序号)。
正确答案
②④
解析
解析已在路上飞奔,马上就到!
知识点
充要条件的判定命题的真假判断与应用正弦定理的应用平行投影及平行投影作图法
1
题型:简答题
|
18.已知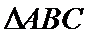
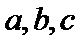
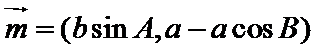
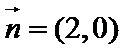
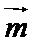
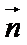
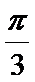
(Ⅰ)求角B的大小;
(Ⅱ)求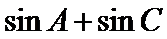
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
三角函数中的恒等变换应用两角和与差的正弦函数正弦定理的应用平面向量数量积的运算
1
题型:简答题
|
16.已知


(1)求角C的大小;
(2)若
正确答案
(1)C= 
(2)a=2,b=4或a=4,b=2
解析
解析已在路上飞奔,马上就到!
知识点
正弦定理的应用余弦定理的应用平面向量共线(平行)的坐标表示
1
题型:简答题
|
17.在



(Ⅰ)求证:
(Ⅱ)若


正确答案
见解析
解析
(Ⅰ)
证明:由正弦定理得:
即

(Ⅱ)


考查方向
解三角形、等差数列
解题思路
第一问根据正弦定理得到三个角的正弦关系,进而建立角与边的关系,第二问利用正弦定理求面积公式求解
易错点
正弦定理误用、化简整理错误
知识点
三角函数中的恒等变换应用二倍角的余弦正弦定理的应用等差数列的判断与证明
1
题型:填空题
|
在锐角△ABC中,若C=2B,则
正确答案
解析
因为锐角△ABC中,若C=2B所以A=180°﹣B
∴
∴30°<B<45°
由正弦定理可得,
∵
∴
知识点
正弦定理的应用
下一知识点 : 余弦定理
扫码查看完整答案与解析


























