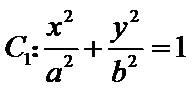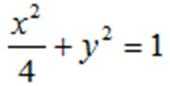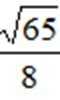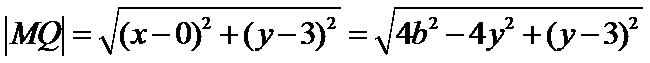椭圆的几何性质
共178题

· 椭圆的几何性质

椭圆的几何性质
共178题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

11．已知椭圆（a＞b＞0）的左、右焦点分别为F1，F2，过F2的直线与椭圆交于A、B两点，若△F1AB是以A为直角顶点的等腰直角三角形，则离心率为

B2－

C－2

D－

正确答案

解析

设F1A=x, F2A=y,由题可知，x+y=2a,x2+y2=4c2,2x+√2x=4a，联立方程组，代换得

a2（9-6√2）=c2,即e=－。A选项不正确，B选项不正确，C选项不正确，所以选D选项。

考查方向

本题主要考查直线与椭圆的位置关系

解题思路

1、用a,c表示出F1A,F2A；

2、将所求式子联立，即可得到结果。A选项不正确，B选项不正确，C选项不正确，所以选D选项。

易错点

本题易在表示a, c关系时发生错误。

知识点

椭圆的几何性质直线与椭圆的位置关系

题型：简答题

简答题 · 14 分

19.已知椭圆:的离心率为，点在椭圆C上，O为坐标原点.

（Ⅰ）求椭圆的方程；

（Ⅱ）设动直线与椭圆有且仅有一个公共点，且与圆相交于不在坐标轴上的两点，，记直线，的斜率分别为，，求证：为定值.

正确答案

（Ⅰ）椭圆的方程为

解析

（Ⅰ）解：由题意，得，，

又因为点在椭圆上，

所以，

解得，，，

所以椭圆C的方程为.

（Ⅱ）证明：当直线的斜率不存在时，由题意知的方程为，

易得直线，的斜率之积.

当直线的斜率存在时，设的方程为.

由方程组得，

因为直线与椭圆C有且只有一个公共点，

所以，即.

由方程组得，

设，，则，，

所以

，

将代入上式，

得.

综上，为定值.

考查方向

本题以焦点在x轴上的椭圆和定圆相关知识为背景，通过直线与其位置关系为纽带设计而成，为历届高考中的高频考点，同时圆锥曲线也是学生分析问题、解决问题及计算等能力检测的重要素材。

解题思路

1、每一问通过椭圆离心率，点在椭圆上和列出方程组即可求出的值从而求出椭圆的方程。

2、第二问求证为定值，通过设，可知，于是可考虑运用韦达定理把表达出来求解，从而得出解题的思路：即当（１）斜率不存在时，求；（２）斜率存在时，设的方程分别与圆、椭圆联立方程组进而求解。

易错点

对于第二问不考虑斜率存在与否直接解答从而导致考虑不全面而失分。

知识点

椭圆的定义及标准方程椭圆的几何性质圆锥曲线的定点、定值问题

题型：填空题

填空题 · 12 分

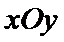
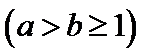
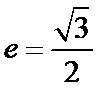
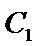
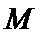
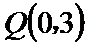
20．在平面直角坐标系中，已知椭圆的离心率，且椭圆上一点到点的距离的最大值为4．

（Ⅰ）求椭圆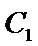的方程；

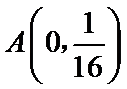
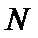
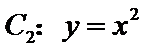
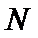
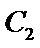
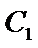
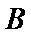
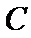
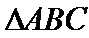
（Ⅱ）设，为抛物线上一动点，过点作抛物线的切线交椭圆于，两点，求面积的最大值．

正确答案

（Ⅰ）

（Ⅱ）

解析

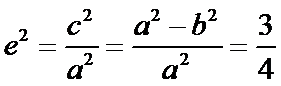
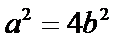
（Ⅰ）因为，所以．

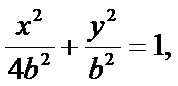
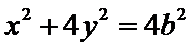
则椭圆方程为即．

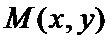
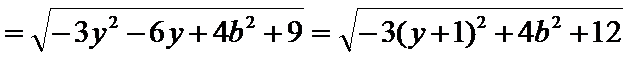
设，则

．

当时，有最大值为．

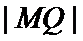
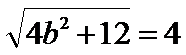
解得，则．

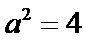
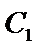
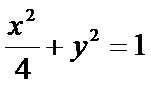
所以椭圆的方程是．

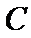
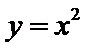
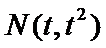
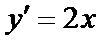
（Ⅱ）设曲线：上的点，因为，

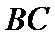
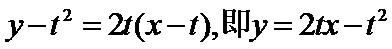
所以直线的方程为：． ①

将①代入椭圆方程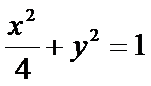中整理，

得．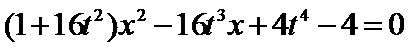

则有．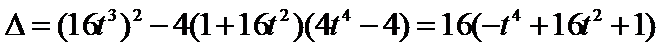

且．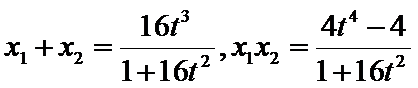

所以

．

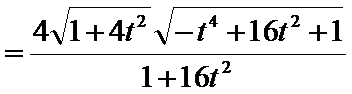
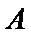
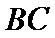
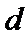
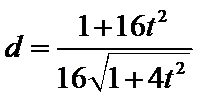
设点到直线的距离为，则．

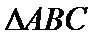
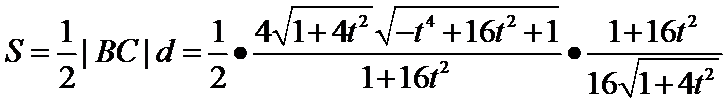
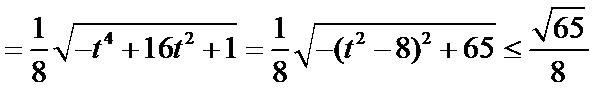
所以的面积．

．

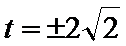
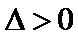
当时取到“=”，经检验此时，满足题意．

综上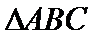，面积的最大值为．

考查方向

本题考查了直线与圆锥曲线的关系，椭圆的标准方程以及二次函数求最值。

解题思路

易错点

第一问未能利用|MQ|最大值求出b;第二问运算量较大，代数式化简容易出错。

知识点

椭圆的定义及标准方程椭圆的几何性质抛物线的标准方程和几何性质圆锥曲线中的范围、最值问题

题型：简答题

简答题 · 12 分

20.椭圆，作直线交椭圆于两点，为线段的中点，为坐标原点，设直线的斜率为，直线的斜率为，.

（1）求椭圆的离心率；

（2）设直线与轴交于点，且满足，当的面积最大时，求椭圆的方程．

正确答案

（1）；

（2）．

解析

试题分析：本题属于椭圆的几何性质、直线与椭圆的位置关系、基本不等式．等知识点的综合应用问题，属于拔高题，第二问不容易得分，解析如下：

（1）设，，代入椭圆C的方程有：

，、

两式相减：，

即，

又，

联立两个方程有，

解得：.

（2）由（1）知，得，

可设椭圆C的方程为：，

设直线l的方程为：，代入椭圆C的方程有

，

因为直线l与椭圆C相交，所以，

由韦达定理：，.

又，所以，

代入上述两式有：，

所以

，

当且仅当时，等号成立，此时，代入，有成立，

所以所求椭圆C的方程为：.

考查方向

本题考查了椭圆的几何性质、直线与椭圆的位置关系、基本不等式等知识点。

解题思路

（1）设，，并分别代入椭圆方程中，然后两式相减，利用直线斜率公式求得，从而求得离心率；

（2）设椭圆的方程为：，直线的方程为：，然后联立椭圆与直线的方程得到关于的二次方程，然后由，及利用韦达定理得出的表达式，从而利用基本不等式求得椭圆的方程．

易错点

知识点

直线的倾斜角与斜率椭圆的定义及标准方程椭圆的几何性质圆锥曲线中的范围、最值问题

题型：简答题

简答题 · 14 分

（14分）（2015•上海）已知椭圆x2+2y2=1，过原点的两条直线l1和l2分别于椭圆交于A、B和C、D，记得到的平行四边形ABCD的面积为S．

（1）设A（x1，y1），C（x2，y2），用A、C的坐标表示点C到直线l1的距离，并证明S=2|x1y2﹣x2y1|；

（2）设l1与l2的斜率之积为﹣，求面积S的值．

正确答案

解：（1）依题意，直线l1的方程为y=x，由点到直线间的距离公式得：点C到直线l1的距离d==，

因为|AB|=2|AO|=2，所以S=|AB|d=2|x1y2﹣x2y1|；

（2）方法一：设直线l1的斜率为k，则直线l2的斜率为﹣，

设直线l1的方程为y=kx，联立方程组，消去y解得x=±，

根据对称性，设x1=，则y1=，

同理可得x2=，y2=，所以S=2|x1y2﹣x2y1|=．

方法二：设直线l1、l2的斜率分别为、，则=﹣，

所以x1x2=﹣2y1y2，

∴=4=﹣2x1x2y1y2，

∵A（x1，y1）、C（x2，y2）在椭圆x2+2y2=1上，

∴（）（）=+4+2（+）=1，

即﹣4x1x2y1y2+2（+）=1，

所以（x1y2﹣x2y1）2=，即|x1y2﹣x2y1|=，

所以S=2|x1y2﹣x2y1|=．

知识点

椭圆的几何性质直线与椭圆的位置关系

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 椭圆的几何性质

扫码查看完整答案与解析