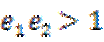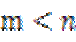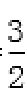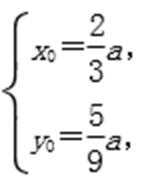- 椭圆的几何性质
- 共178题
7.已知椭圆



正确答案
解析
.由题意知




考查方向
解题思路
根据焦点重合找出m,n的关系,

易错点
离心率之积的判断会出错。
知识点
已知椭圆








24. 设






25. 设



26. 设






正确答案
(1)略
解析
试题分析:(1)依题意,直线l1的方程
(1)直线

由点到直线的距离公式得点


因为
所以
考查方向
解题思路
直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查,一直是高考考查的重点,特别是焦点弦和中点弦等问题,涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法,也是考查数学思想方法的热点题型.
易错点
准确计算化简
正确答案
((2)

解析
试题分析:(2)由(1)得:
(2)由


由(1)得
由题意知
解得

考查方向
解题思路
直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查,一直是高考考查的重点,特别是焦点弦和中点弦等问题,涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法,也是考查数学思想方法的热点题型.
易错点
面积公式的恰当选取运用
正确答案
(3)
解析
试题分析:(3)设直线l1的斜率为k,则直线l1的方程为y=kx,联立方程组







得到
(3)设



由

同理
由(1)知,

整理得
由题意知

则

所以
考查方向
解题思路
直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查,一直是高考考查的重点,特别是焦点弦和中点弦等问题,涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法,也是考查数学思想方法的热点题型.当直线(斜率为k)与圆锥曲线交于点A(x1,y1),B(x2,y2)时,则|AB|=


易错点
化简计算及方程恒成立问题
平面直角坐标系




24.求椭圆C的方程;
25.设椭圆E:

(i)求
(ii)求
正确答案

解析
(I)由题意知

又

所以椭圆

考查方向
解题思路
(Ⅰ)运用椭圆的离心率公式和a,b,c的关系,计算即可得到b,进而得到椭圆C的方程;
易错点
椭圆方程中系数的求解
正确答案
2,
解析
【解析】 (II)由(I)知椭圆
(i)设

因为


所以 

(ii)设
将

可得
由 
则有
所以
因为 直线


所以 
令


可得 
由
由①②可知 
因此

当且仅当


由(i)知,

所以 

考查方向
解题思路
(Ⅱ)求得椭圆E的方程,(i)设P(x0,y0),|
(ii)设A(x1,y1),B(x2,y2),将直线y=kx+m代入椭圆E的方程,运用韦达定理,三角形的面积公式,将直线y=kx+m代入椭圆C的方程,由判别式大于0,可得t的范围,结合二次函数的最值,又△ABQ的面积为3S,即可得到所求的最大值.
易错点
直线与圆锥曲线的综合问题;椭圆的标准方程;曲线与方程.菁优网版权所有
一种画椭圆的工具如图1所示.







26.求椭圆C的方程;
27.设动直线






正确答案
(Ⅰ)
解析
(Ⅰ)因为







考查方向
解题思路
(Ⅰ)由题意并结合三角形三边关系(两边之和大于第三边,两边之差小于第三边)知,





易错点
粗心算错。
正确答案
(Ⅱ)当直线


解析
(Ⅱ)(1)当直线




(2)当直线








又由







将①代入②得,











综合(1)(2)可知,当直线


考查方向
解题思路
(Ⅱ)首先讨论直线






























易错点
忘记讨论斜率不存在的情况。
已知抛物线











23.分别求抛物线

24.经过








正确答案
见解析
解析
由已知抛物线



设椭圆






考查方向
解题思路
第一问根据离心率及焦点求抛物线C和椭圆E的方程,第二问利用平面向量的数量积的坐标公式证明线段和线段垂直。
易错点
计算错误,利用平面向量证明线段垂直
正确答案
见解析
解析
显然直线


故可设直线


由



∵抛物线


∴过抛物线



即

解得两条切线




∴
考查方向
解题思路
第一问根据离心率及焦点求抛物线C和椭圆E的方程,第二问利用平面向量的数量积的坐标公式证明线段和线段垂直。
易错点
计算错误,利用平面向量证明线段垂直
在平面直角坐标系xOy中,点C在椭圆M: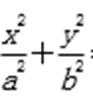
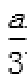
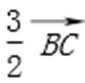
20.求椭圆M的离心率;
21.设椭圆M的焦距为4,P,Q是椭圆M上不同的两点,线段PQ的垂直平分线为直线l,且直线l不与y轴重合.
①若点P(-3,0),直线l过点(0,-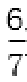
②若直线l过点(0,-1) ,且与x轴的交点为D,求D点横坐标的取值范围.
正确答案
(1)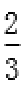
解析
解:(1)设C (x0,y0),则
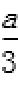
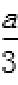
因为
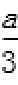
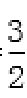
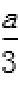

得
代入椭圆方程得a2=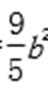
因为a2-b2=c2,所以e=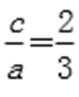
考查方向
解题思路
本题考查直线与椭圆位置关系,解题步骤如下:
(1)设C(m,n),由向量共线的坐标表示,可得C的坐标,代入椭圆方程,可得a,b的关系,
再由离心率公式计算即可得到所求值;
(2)①由题意可得c=2,a=3, b2=5,可得椭圆方程,设直线PQ的方程为y=k(x+3),代入椭圆方程,运用韦达定理和中点坐标公式,再由两直线垂直的条件:斜率之积为-1,解方程可得k,进而得到所求直线方程;
②设直线PQ的方程为y=kx+m,代入椭圆方程可得,运用韦达定理和中点坐标公式,再由两直线垂直的条件,求得4m=5+9k2,再由中点在椭圆内,可得k的范围,再由直线l的方程可得D的横坐标的范围.
易错点
第二问容易计算错误
正确答案
(2)①y=-x+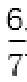

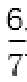
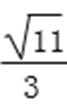
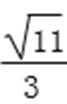
解析
解:(2)①因为c=2,所以a2=9,b2=5,所以椭圆的方程为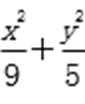
设Q (x0,y0),则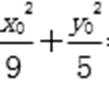
因为点P(-3,0),所以PQ中点为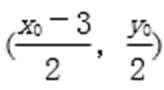
因为直线l过点(0,-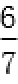
所以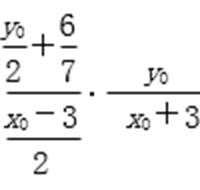
化简得x02=9-y02-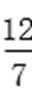
将②代入①化简得y02-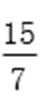
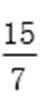
将y0=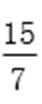
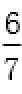
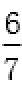
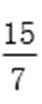
所以PQ斜率为1或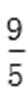
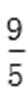
所以直线l的方程为y=-x+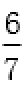
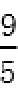
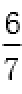
②设PQ:y=kx+m,则直线l的方程为:y=-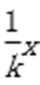
将直线PQ的方程代入椭圆的方程,消去y得(5+9k2)x2+18kmx+9m2-45=0.…………①,
设P(x1,y1),Q(x2,y2),中点为N,
xN=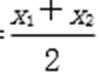
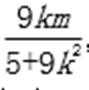
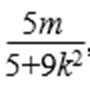
代入直线l的方程得9k2=4m-5. ……②
又因为△=(18km)2-4(5+9k2) (9m2-45)>0,
化得m2-9k2-5<0.
将②代入上式得m2-4m<0,解得0<m<4,
所以-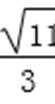
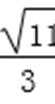
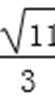
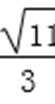
综上所述,点D横坐标的取值范围为(-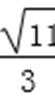
考查方向
解题思路
本题考查直线与椭圆位置关系,解题步骤如下:
(1)设C(m,n),由向量共线的坐标表示,可得C的坐标,代入椭圆方程,可得a,b的关系,
再由离心率公式计算即可得到所求值;
(2)①由题意可得c=2,a=3, b2=5,可得椭圆方程,设直线PQ的方程为y=k(x+3),代入椭圆方程,运用韦达定理和中点坐标公式,再由两直线垂直的条件:斜率之积为-1,解方程可得k,进而得到所求直线方程;
②设直线PQ的方程为y=kx+m,代入椭圆方程可得,运用韦达定理和中点坐标公式,再由两直线垂直的条件,求得4m=5+9k2,再由中点在椭圆内,可得k的范围,再由直线l的方程可得D的横坐标的范围.
易错点
第二问容易计算错误
已知抛物线C











24.求C
25.若|AC|=|

正确答案
解析
由


所以 















考查方向
解题思路
根据已知条件可求得


易错点
不会转化题中给出的条件

正确答案

考查方向
易错点
1.第(2)问联立方程运算出错;
阅读下面这首宋诗,完成8—9题。
野泊对月有感
周莘
可怜江月乱中明,
应识逋逃①病客情。
斗柄阑干洞庭野,
角声凄断岳阳城。
酒添客泪愁仍溅,
浪卷归心暗自惊。
欲问行朝②近消息,
眼中群盗尚纵横。
【注释】①逋逃:愤激之词,意为飘泊无家。②行朝:迁徙不定的朝廷。
8.后人评价认为周莘此诗颔联写景很有特色,在写景上与李贺的诗《雁门太守行》第三四两句有异曲同工之妙,请结合诗句内容具体分析周诗颔联与《雁门太守行》第三四两句在写景手法上的相同之处。
9.本诗最后两联联表达了诗人的什么情感?请结合诗句作简要分析。
正确答案
两首诗都运用了动静结合(或视听结合)手法。(2)①周诗颔联前一句写静景(视觉),诗人立于洞庭荒野,仰望天空北斗横斜;后一句写动景(听觉),耳畔传来岳阳城凄凉的角声,暗指兵荒马乱,动静结合,渲染了空茫凄凉的意境。 ②李诗颔联前一句诗从听觉描写,在深秋死寂中满城响起角声;后一句从视觉描写,夜晚晚霞映照战场,胭脂般的血迹凝结在大地上,呈现一片紫色;视听结合(动静结合)渲染出战地的悲壮气氛和战争残酷。
解析
周诗的第三句写诗人立于洞庭荒野,仰望天空北斗横斜。“斗柄”指北斗的第五至第七星,即衡、开泰、摇光。北斗,第一至第四星象斗,第五至第七星象柄。“阑干”指横斜貌。三国 魏 曹植 《善哉行》:"月没参横,北斗阑干"。第四句写耳畔传来岳阳城凄凉的角声。综合考虑可以看出运用了动静结合的手法。
《雁门太守行》三四句为“角声满天秋色里,塞上燕脂凝夜紫”。意为号角的声音在这秋色里响彻天空;夜色中,塞上泥土中鲜血浓艳得如紫色。和周诗比较就可得知相同的手法即为动静结合。结合诗句分析作答即可。
考查方向
解题思路
回答时结合诗句点明修辞手法并具体分析,后简洁点明效果。
易错点
不结合诗句作具体分析
正确答案
(1)漂泊思归之情。 “酒添客泪”写出了诗人身在客中,不由伤感落泪,想要借酒浇愁,却依旧愁心难抑, “归心”则透露了诗人的思归之情。(2)忧国伤时之情。 “欲问行朝近消息”一句表现了诗人对朝廷的关切, “眼中盗贼尚纵横”一句则勾勒出遍地兵荒马乱的景象。
解析
根据题目和注释可知本诗是一首羁旅诗。通过“客泪” “归心”可看出思归之情;“欲问行朝近消息”一句表现了诗人对朝廷的关切,即忧国之情。“眼中盗贼尚纵横”一句则勾勒出遍地兵荒马乱的景象,即感时伤世之情。
考查方向
解题思路
结合诗句的最后两联具体分析
易错点
不结合诗句具体分析,只是空谈。
已知椭圆

24.求椭圆
25.设直线









正确答案

解析
试题分析:本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,由方程思想求解出标准方程; 由已知设椭圆


由



考查方向
解题思路
本题考查圆锥曲线中求标准方程的方法和最值问题——函数思想,解题步骤如下:由方程思想求解出标准方程;
易错点
无法构建关于点

正确答案
解析
试题分析:本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,(构建关于点




则由



设点

∵四边形





从而

又点


当且仅当
当直线


从而点







∴点


考查方向
解题思路
本题考查圆锥曲线中求标准方程的方法和最值问题——函数思想,解题步骤如下:构建关于点

易错点
运算和斜率不存在的讨论。
已知中心在坐标原点,焦点在





23.求椭圆
24.若







正确答案

解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:由题意知






考查方向
解题思路
利用相关知识求椭圆方程;
易错点
对题中条件的处理容易出错。
正确答案

解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:设









因为


整理得
所以





考查方向
解题思路
联立方程组,利用题中所给条件找关系,整理即可求解.
易错点
对题中条件的处理容易出错。
扫码查看完整答案与解析