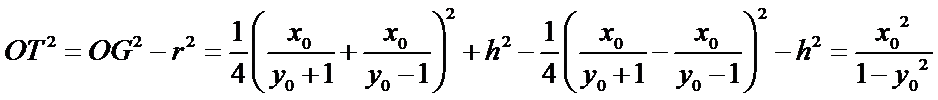- 椭圆的几何性质
- 共178题
已知椭圆



23.求椭圆C的方程;
24.设不过原点O的直线
PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围。
正确答案
(1)
解析
:(1) 由直线



由

又

椭圆C的方程为
考查方向
解题思路
问先根据


易错点
不会转化

正确答案
(2)(0,1)
解析
:
(2)由题意可知,直线
y=kx+m(m≠0),P(x1,y1),Q(x2,y2),
由消去y得(1+4k2)x2+8kmx+4(m2-1)=0,
则Δ=64k2m2-16(1+4k2)(m2-1)=16(4k2-m2+1)>0,
且x1+x2=,x1x2=.
故y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.
因为直线OP,PQ,OQ的斜率依次成等比数列,
所以·==k2,
即+m2=0, 又m≠0,所以k2=,即k=±.
由Δ>0,及直线OP,OQ的斜率存在,得0<m2<2且m2≠1.
S△OPQ=|x1-x2||m|= 
所以S△OPQ的取值范围为(0,1).
考查方向
解题思路
设出直线


易错点
不会转化OP,PQ,OQ的斜率依次成等比数列导致问题找不到突破口。
已知椭圆


且 
23.求椭圆E的方程;
24.过点P的直线
(i)若

(ii)在y轴上是否存在与点P不同的定点Q,使得
正确答案
考查方向
解题思路
由题意,根据数量积求得方程中的待定的a,b.(2).按照解析几何的常规思路求解,
先讨论直线方程的斜率问题,然后联系方程组,求方程的
易错点
解析几何易出现对于直线方程的分类讨论上的错,再就是直线与曲线联系以后,寻求变量之间的联系时,易出现转化和计算,代数整理上的错误。
正确答案
解析
解:(1)当直线不存在斜率时,|PB|=


考查方向
解题思路
也是要讨论直线方程的斜率两种情况,假设存在,Q,使得
易错点
解析几何易出现对于直线方程的分类讨论上的错,再就是直线与曲线联系以后,寻求变量之间的联系时,易出现转化和计算,代数整理上的错误。
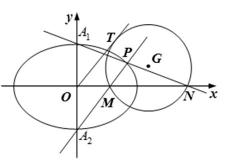
如图,已知椭圆



22.求椭圆
23. 若过点






正确答案
解析
解: 由已知可得, 
所求椭圆的方程为
考查方向
解题思路
列出a,b,c方程, 直接求椭圆的标准方程
易错点
解析几何易出现对于直线方程的分类讨论上的错误,其次就是直线与曲线联系以后,寻求变量之间的关系时,易出现转化、计算、代数整理的错误。
正确答案
直线

解析
解:设切线方程为


设两切线



由


同理可得:
所以




故直线

考查方向
解题思路
首先根据直线与圆相切得出
易错点
解析几何易出现对于直线方程的分类讨论上的错误,其次就是直线与曲线联系以后,寻求变量之间的关系时,易出现转化、计算、代数整理的错误。
已知椭圆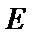
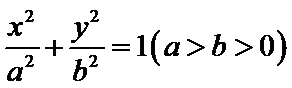
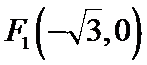
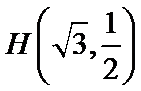
求椭圆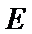
设椭圆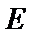
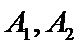
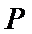
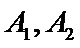
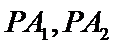
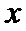
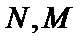
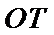
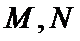
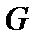
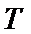
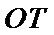
为定值,并求出该定值.
正确答案
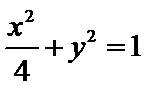
解析
试题分析:本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,由方程思想求解出标准方程;
解法一:由题意得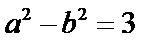
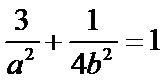
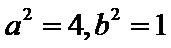
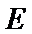
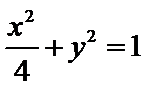
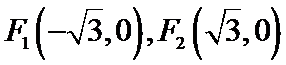
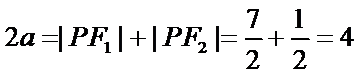
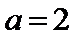


考查方向
解题思路
本题考查圆锥曲线中求标准方程的方法和定值问题,解题步骤如下:由方程思想求解出标准方程;
易错点
无法理顺题设的关系导致解题受阻。
正确答案
解析
试题分析:本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,根据题设求出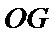
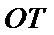
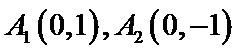
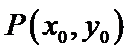
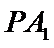
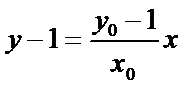
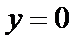
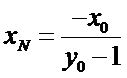
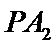
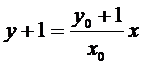
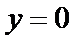
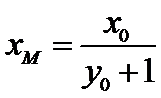
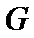
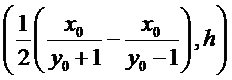
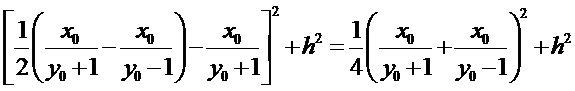
而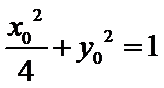

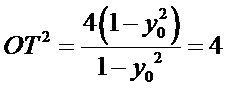
所以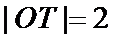
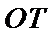
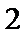
解法二:由(Ⅰ)可知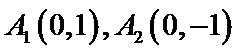
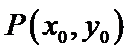
直线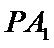
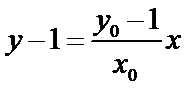
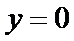
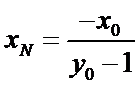
直线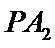
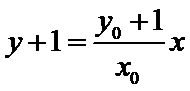
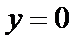
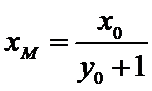
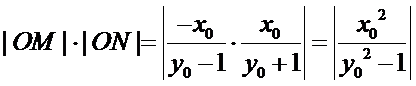
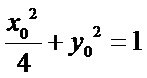
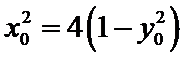
所以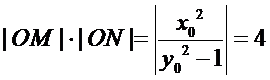

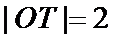
考查方向
解题思路
本题考查圆锥曲线中求标准方程的方法和定值问题,解题步骤如下:构建
易错点
无法理顺题设的关系导致解题受阻。
已知椭圆




24.求直线

25.过点






正确答案
直线


解析
由题可得

则有
考查方向
解题思路
解题步骤如下:由椭圆的方程,可得到A ,B两点的坐标,设出点P(x,y),即可表示出直线

易错点
本题是综合性比较强的大题,涉及到的的知识点比较多,计算量较大,所以在计算时易发生错误 。
正确答案
见解析
解析
设





由题意,可知


∴


考查方向
解题思路
解题步骤如下:要证明以





易错点
本题是综合性比较强的大题,涉及到的的知识点比较多,计算量较大,所以在计算时易发生错误 。
扫码查看完整答案与解析