椭圆的几何性质
共178题

· 椭圆的几何性质

椭圆的几何性质
共178题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：单选题

单选题 · 5 分

有一个容量为66的样本，数据的分组及各组的频数如下：

根据样本的频率分布估计，数据落在[31.5，43.5)的概率约是

正确答案

解析

从到共有22，所以。

知识点

椭圆的几何性质

题型：填空题

填空题 · 5 分

已知椭圆C：，点M与C的焦点不重合，若M关于C的焦点的对称点分别为A，B，线段MN的中点在C上，则 .

正确答案

解析

如图：MN的中点为Q，易得，，

∵Q在椭圆C上，∴|QF1|+|QF2|=2a=6，

∴|AN|+|BN|=12。

知识点

椭圆的几何性质

题型：简答题

简答题 · 13 分

在平面直角坐标系中，点为动点，，

分别为椭圆的左右焦点，已知为等腰三角形。

（1）求椭圆的离心率；

（2）设直线与椭圆相交于两点，是直线上的点，满足，求点的轨迹方程。

正确答案

（1）椭圆的离心率为

（2）点的轨迹方程为，。

解析

（1）设，，因为为等腰三角形，

若，则点在轴上，与矛盾，

若，则，，

由，有，即，或，不合题意，

所以，则，，

由，有，即，（舍去）或。

所以椭圆的离心率为。

（2）解法1。因为，所以，，所以椭圆方程为。

直线的斜率，则直线的方程为。

两点的坐标满足方程组

消去并整理得，则，。

于是　不妨设，。

设点的坐标为，则，，

由得，则

，。

由，得，

化简得。

将代入得，所以。

因此点的轨迹方程为，。

解法2。因为，所以，。

椭圆方程为。

直线的斜率，则直线的方程为。

两点的坐标满足方程组

消去并整理得，则，。

于是　不妨设，。

因而点为椭圆短轴的下顶点。

如图，因为，所以点在线段的内部，

设点的坐标为，则。

过和作轴的垂线，垂足分别为。

因为，，则，

于是，。

因为，是直线上的点，则，

所以，即，

，。

由得，则，。

，于是，。

因此点的轨迹方程为，。

解法3。因为，所以，，所以椭圆方程为。

直线的斜率，则直线的方程为。

两点的坐标满足方程组

消去并整理得。

设，，则　　　　　　　　　　①

，

。

则　　　　　　　　　　　　　　　　　　　　②

因为，所以，

，　　　③

将①，②代入式③得

，　　　　　　④

将代入④并整理得。

将代入得，所以。

因此点的轨迹方程为，。

知识点

椭圆的几何性质

题型：单选题

单选题 · 5 分

若实数a，b满足，则称a与b互补，记，那么是a与b互补的

A充分而不必要条件

B必要而不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

，故至少有一个为0，不妨设，由，于是，同理可证：，故互补；反之若互补，由，不妨设则，即。综上。是a与b互补的充要条件。

知识点

椭圆的几何性质

题型：简答题

简答题 · 12 分

正确答案

(1) C的离心率为.

(2)

解析

知识点

椭圆的几何性质直线与椭圆的位置关系直线、圆及圆锥曲线的交汇问题

题型：填空题

填空题 · 4 分

计算。

正确答案

解析

知识点

椭圆的几何性质

题型：填空题

填空题 · 5 分

从这4个数中一次随机地取2个数，则所取2个数的乘积为6的概率是。

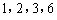
正确答案

解析

略

知识点

椭圆的几何性质

题型：填空题

填空题 · 5 分

如图，已知AB和AC是圆的两条弦，过点B作圆的切线与AC的延长线相交于点D. 过点C作BD的平行线与圆相交于点E，与AB相交于点F，AF=3，FB=1，EF=，则线段CD的长为____________

正确答案

解析

知识点

椭圆的几何性质

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 椭圆的几何性质

扫码查看完整答案与解析