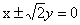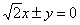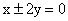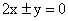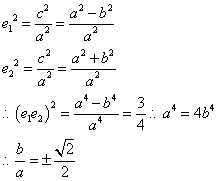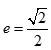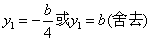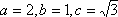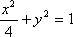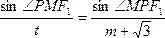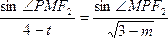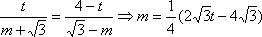- 椭圆的几何性质
- 共178题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知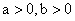
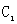
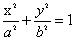

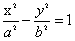
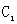
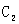
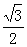
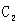
正确答案
解析
知识点
设椭圆C:

(1)求椭圆C的离心率;
(2)如果|AB|=
正确答案
(1)
解析
设


(1)直线l的方程为 

联立
解得
因为

即
得离心率 
(2)因为

由



椭圆C的方程为
知识点
已知椭圆C:

正确答案
解析
如图所示。
根据余弦定理|AF|2=|BF|2+|AB|2-2|AB|·|BF|cos∠ABF,即|BF|2-16|BF|+64=0,得|BF|=8.
又|OF|2=|BF|2+|OB|2-2|OB|·|BF|cos ∠ABF,得|OF|=5.
根据椭圆的对称性|AF|+|BF|=2a=14,得a=7.
又|OF|=c=5,故离心率e=
知识点
如图,椭圆C:


(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,说明理由。
正确答案
(1) 
解析
(1)由P

依题设知a=2c,则b2=3c2,②
②代入①解得c2=1,a2=4,b2=3.
故椭圆C的方程为
(2)方法一:由题意可设AB的斜率为k,
则直线AB的方程为y=k(x-1),③
代入椭圆方程3x2+4y2=12并整理,得(4k2+3)x2-8k2x+4(k2-3)=0.
设A(x1,y1),B(x2,y2),则有
x1+x2=

在方程③中令x=4得,M的坐标为(4,3k)。
从而


注意到A,F,B共线,则有k=kAF=kBF,即有
所以k1+k2=

④代入⑤得k1+k2=
又k3=
故存在常数λ=2符合题意。
(2)方法二:设B(x0,y0)(x0≠1),则直线FB的方程为:
令x=4,求得M
从而直线PM的斜率为
联立
得A
则直线PA的斜率为:

所以k1+k2=
故存在常数λ=2符合题意
知识点
设椭圆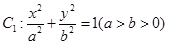
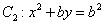
(1)若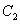
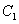
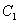
(2)设A(0,b),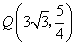
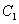
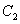
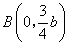
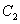
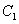
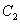
正确答案
(1)
解析
(1)由已知椭圆焦点(c,0)在抛物线上,可得: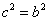
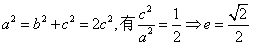
(2)由题设可知M、N关于y轴对称,设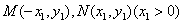
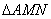
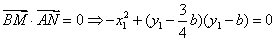
由点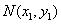
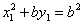
故
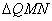

由重心在抛物线上得: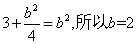
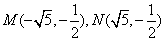
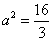
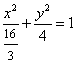
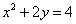
知识点
椭圆
正确答案
解析
因为A,B为左、右顶点,F1,F2为左、右焦点,
所以|AF1|=a-c,|F1F2|=2c,|BF1|=a+c.
又因为|AF1|,|F1F2|,|BF1|成等比数列,
所以(a-c)(a+c)=4c2,即a2=5c2,
所以离心率
知识点
椭圆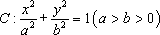
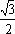



(1)求椭圆
(2)点
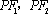
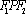
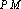
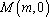

(3)在(2)的条件下,过点
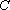
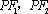
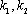
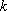
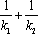
正确答案
见解析。
解析
(1)由已知的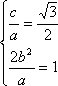
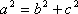
所以椭圆的标准方程为
(2)设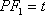
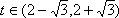
在三角形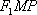
同理,在三角形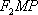
而且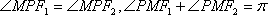
所以
知识点
如图,椭圆E:

(1)求椭圆E的方程。
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相较于点Q,试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由。
正确答案
(1)E的方程为
(2)满足条件的点M存在,只能是M(1,0)
解析
(1)∵过F1的直线交椭圆于A、B两点,且△ABF2的周长为8。
∴4a=8,∴a=2
∵e=
∴b2=a2﹣c2=3
∴椭圆E的方程为
(2)由
∵动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0,y0)
∴m≠0,△=0,∴(8km)2﹣4×(4k2+3)×(4m2﹣12)=0
∴4k2﹣m2+3=0①
此时x0=




由
取k=0,m=



取k=




故若满足条件的点M存在,只能是M(1,0),证明如下
∵
∴
故以PQ为直径的圆恒过y轴上的定点M(1,0)
知识点
在平面直角坐标系






(1)求椭圆
(2) 在椭圆







正确答案
(1) 

(2) 存在,面积最大为





解析
(1)依题意

设



所以
当



故椭圆

(2)[韦达定理法]因为




由
所以

由韦达定理得
所以
所以
设原点


所以
设



所以,当


此时,点




[垂径定理切入]因为点



圆心


直线

所以
知识点
扫码查看完整答案与解析