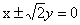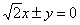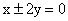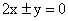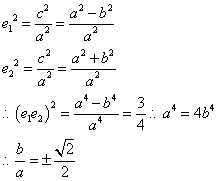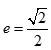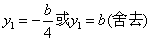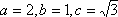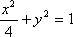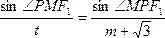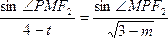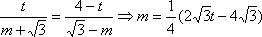- 椭圆的几何性质
- 共178题
已知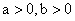
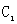
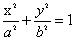

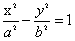
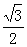
正确答案
解析
知识点
设椭圆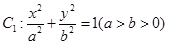
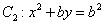
(1)若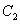
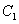
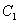
(2)设A(0,b),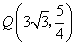
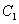
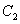
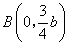
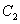
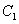
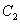
正确答案
(1)
解析
(1)由已知椭圆焦点(c,0)在抛物线上,可得: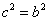
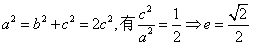
(2)由题设可知M、N关于y轴对称,设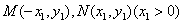
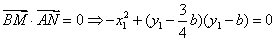
由点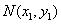
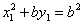
故
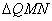

由重心在抛物线上得: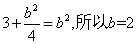
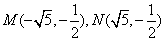
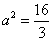
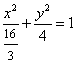
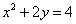
知识点
椭圆
正确答案
解析
因为A,B为左、右顶点,F1,F2为左、右焦点,
所以|AF1|=a-c,|F1F2|=2c,|BF1|=a+c.
又因为|AF1|,|F1F2|,|BF1|成等比数列,
所以(a-c)(a+c)=4c2,即a2=5c2,
所以离心率
知识点
椭圆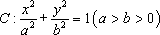
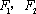
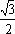


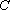

(1)求椭圆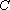
(2)点
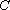
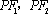
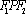
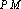
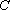
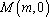

(3)在(2)的条件下,过点
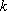
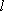
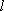
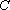
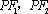
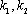
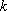
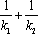
正确答案
见解析。
解析
(1)由已知的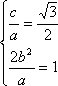
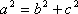
所以椭圆的标准方程为
(2)设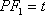
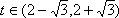
在三角形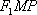
同理,在三角形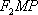
而且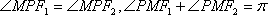
所以
知识点
在平面直角坐标系






(1)求椭圆
(2) 在椭圆







正确答案
(1) 

(2) 存在,面积最大为





解析
(1)依题意

设



所以
当



故椭圆

(2)[韦达定理法]因为




由
所以

由韦达定理得
所以
所以
设原点


所以
设



所以,当


此时,点




[垂径定理切入]因为点



圆心


直线

所以
知识点
扫码查看完整答案与解析