- 椭圆的几何性质
- 共178题
设






正确答案
解析


知识点
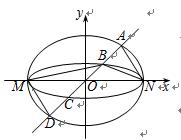
如图,已知椭圆
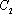

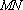

为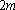
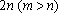

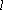
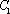
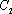
大到小依次为A,B,C,D,记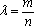
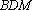
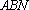
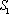
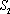
(1)当直线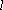
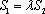
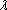
(2)当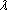
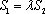
正确答案
(1)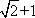

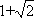
解析
依题意可设椭圆C1和C2的方程分别为
C1: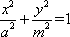
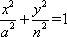
其中a>m>n>0,λ=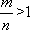
(1)解法1:
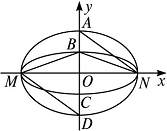
如图1,若直线l与y轴重合,即直线l的方程为x=0,则S1=



所以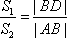
在C1和C2的方程中分别令x=0,可得yA=m,yB=n,yD=-m,
于是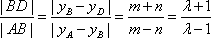
若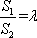
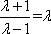
由λ>1,可解得λ=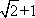
故当直线l与y轴重合时,若S1=λS2,则λ=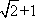
解法2:如图1,若直线l与y轴重合,则
|BD|=|OB|+|OD|=m+n,|AB|=|OA|-|OB|=m-n;
S1=

S2=

所以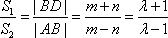
若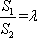
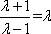
由λ>1,可解得λ=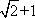
故当直线l与y轴重合时,若S1=λS2,则λ=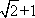
(2)解法1:
如图2,若存在与坐标轴不重合的直线l,使得S1=λS2.根据对称性,不妨设直线l:y=kx(k>0),点M(-a,0),N(a,0)到直线l的距离分别为d1,d2,则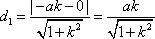
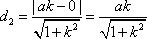
又S1=

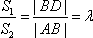
由对称性可知|AB|=|CD|,所以|BC|=|BD|-|AB|=(λ-1)|AB|,
|AD|=|BD|+|AB|=(λ+1)|AB|,于是
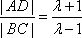
将l的方程分别与C1,C2的方程联立,可求得
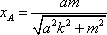
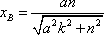
根据对称性可知xC=-xB,xD=-xA,于是
=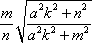
从而由①和②式可得
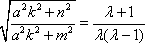
令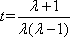
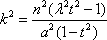
因为k≠0,所以k2>0.于是③式关于k有解,当且仅当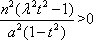
等价于

即
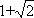
当1<λ≤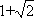
当λ>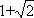
解法2:如图2,若存在与坐标轴不重合的直线l,使得S1=λS2.根据对称性,不妨设直线l:y=kx(k>0),
点M(-a,0),N(a,0)到直线l的距离分别为d1,d2,
则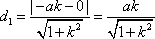
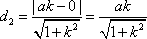
又S1=

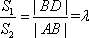
因为
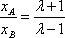
由点A(xA,kxA),B(xB,kxB)分别在C1,C2上,可得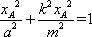
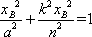
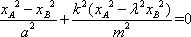
依题意xA>xB>0,所以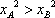
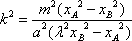
因为k2>0,所以由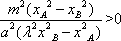
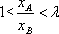
从而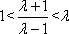
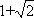
当1<λ≤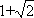
当λ>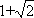
知识点
设D,E分别是△ABC的边AB,BC上的点,


正确答案
解析
由题意作图如图。
∵在△ABC中,



故λ1+λ2=
知识点
已知a=(cos α,sin α),b=(cos β,sin β),0<β<α<π。
(1)若|a-b|=
(2)设c=(0,1),若a-b=c,求α,β的值。
正确答案
见解析
解析
(1)证明:由题意得|a-b|2=2,即(a-b)2=a2-2a·b+b2=2.
又因为a2=b2=|a|2=|b|2=1,
所以2-2a·b=2,即a·b=0.
故a⊥b.
(2)解:因为a+b=(cos α+cos β,sin α+sin β)=(0,1),所以
由此得cos α=cos(π-β),由0<β<π,得0<π-β<π,又0<α<π,故α=π-β.代入sin α+sin β=1,得sin α=sin β=


知识点
已知A,B,C是椭圆W:
(1)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积;
(2)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由。
正确答案
见解析
解析
(1)椭圆W:
因为四边形OABC为菱形,所以AC与OB相互垂直平分。
所以可设A(1,m),代入椭圆方程得

所以菱形OABC的面积是


(2)假设四边形OABC为菱形。
因为点B不是W的顶点,且直线AC不过原点,所以可设AC的方程为y=kx+m(k≠0,m≠0)。
由
设A(x1,y1),C(x2,y2),
则

所以AC的中点为M
因为M为AC和OB的交点,所以直线OB的斜率为
因为k·
所以OABC不是菱形,与假设矛盾。
所以当点B不是W的顶点时,四边形OABC不可能是菱形。
知识点
扫码查看完整答案与解析