- 椭圆的几何性质
- 共178题
在平面直角坐标系中,倾斜角为
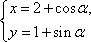
正确答案
ρ(cos θ-sin θ)=1
解析
由题意得曲线C的方程为(x-2)2+(y-1)2=1.
又|AB|=2,故直线l过曲线C的圆心(2,1),则直线方程为y-1=x-2,
即x-y-1=0,故直线l的极坐标方程为ρ(cos θ-sin θ)=1.
知识点
为强化安全意识,某商场拟在未来的连续



正确答案
解析
知识点
如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形。
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1-OB1-D的余弦值。
正确答案
见解析。
解析
(1)
证明:如图(a),因为四边形ACC1A1为矩形,所以CC1⊥AC.同理DD1⊥BD.
因为CC1∥DD1,
所以CC1⊥BD.
而AC∩BD=O,
因此CC1⊥底面ABCD.
由题设知,O1O∥C1C.故O1O⊥底面ABCD.
(2)解法1:如图(a),过O1作O1H⊥OB1于H,连接HC1.
由(1)知,O1O⊥底面ABCD,
所以O1O⊥底面A1B1C1D1,于是O1O⊥A1C1.
又因为四棱柱ABCD-A1B1C1D1的所有棱长都相等,所以四边形A1B1C1D1是菱形,因此A1C1⊥B1D1,从而A1C1⊥平面BDD1B1,所以A1C1⊥OB1,于是OB1⊥平面O1HC1,进而OB1⊥C1H.
故∠C1HO1是二面角C1-OB1-D的平面角。
不妨设AB=2.因为∠CBA=60°,
所以

在Rt△OO1B1中,易知
而O1C1=1,于是
故
即二面角C1-OB1-D的余弦值为
解法2:因为四棱柱ABCD-A1B1C1D1的所有棱长都相等,所以四边形ABCD是菱形,因此AC⊥BD.又O1O⊥底面ABCD,从而OB,OC,OO1两两垂直。
如图(b),以O为坐标原点,OB,OC,OO1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系O-xyz.不妨设AB=2.因为∠CBA=60°,所以

易知,n1=(0,1,0)是平面BDD1B1的一个法向量。
设n2=(x,y,z)是平面OB1C1的一个法向量,则
取


设二面角C1-OB1-D的大小为θ,易知θ是锐角,于是
cos θ=|cos〈n1,n2〉|=
故二面角C1-OB1-D的余弦值为
解题思路
在第(1)问中,从“四边形ACC1A1,BDD1B1均为矩形”出发可证得四棱柱的一条侧棱与底面ABCD的两条对角线垂直,则该侧棱与底面ABCD垂直,而OO1与任一侧棱平行,因此可证得OO1⊥底面ABCD.在第(2)问中可利用两种方法求解,第1种方法为几何法,首先由点O1向二面角的棱B1O作垂线,再将垂足H与C1连接,然后通过线面垂直的性质等证明∠C1HO1即为所求二面角的平面角,最后再在直角三角形中,通过三角函数求得二面角的余弦值;第2种方法为空间向量法,先根据条件证得OB,OC,OO1两两垂直,从而以O为原点建立空间直角坐标系,然后分别求出二面角的两个面的法向量,利用向量的夹角公式即可求得二面角的余弦值。
知识点
若
正确答案
0
解析

知识点
已知函数f(x)=
(1)若x≥0时,f(x)≤0,求λ的最小值;
(2)设数列{an}的通项

正确答案
见解析。
解析
(1)解:由已知f(0)=0,f′(x)=
若
若
综上,λ的最小值是
(2)证明:令
即
取

于是
=
=ln 2n-ln n=ln 2.
所以
知识点
扫码查看完整答案与解析








