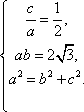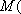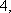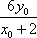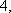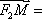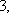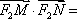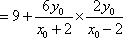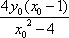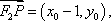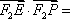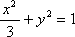- 椭圆的几何性质
- 共178题
已知椭圆





(1)求椭圆
(2)设过点






使


正确答案
(1)
(2)存在定点

解析
(1)解:由 

依题意△


所以椭圆

(2)解:设



将直线

消去

所以 

若



所以
设

将 

整理得 
所以 
将 

整理得 
由于上式对任意实数

综上,存在定点


知识点
若



正确答案
解析
略
知识点
已知椭圆




(1)求椭圆
(2)设椭圆










(3)设O为坐标原点,取

正确答案
见解析
解析
解:(1)解:由



由题意可知

解方程组

所以椭圆C1的方程是
(2)因为







所以点


(3)因为以


设S (











所以
因为


所以
当且仅当

圆的直径|OS|=
因为



所以所求圆的面积的最小时,点S的坐标为(16,±8)
知识点
已知椭圆C:


(1)求椭圆E的标准方程;
(2)如果斜率为
(3) 试求三角形AEF面积S取得最大值时,直线EF的方程。
正确答案
见解析。
解析
(1)由题意,
椭圆


又



(2)设直线

得:


设


分子为:
又


即,直线

(3)





所以直线方程为
知识点
已知椭圆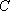
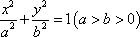

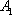
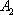
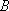
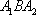
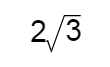
(1)求椭圆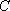

(2)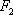
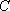
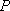
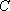
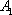
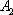
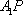
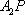
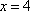
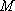
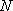
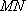
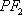
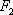
正确答案
见解析
解析
(1)解:由已知
解得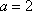
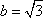
故所求椭圆方程为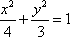
(2)证明:由(1)知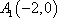
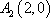
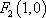
设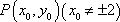
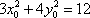
于是直线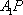
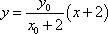
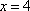
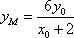
所以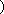
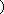
所以
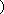
所以
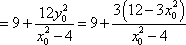
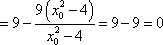
所以 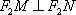
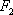
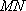
设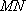
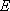
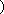
又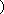
所以
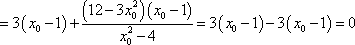
所以 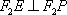
因为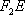
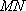
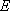
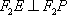
故以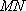
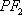
知识点
已知椭圆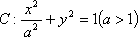
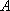
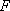
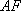
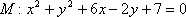
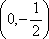
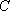
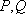
(1)求椭圆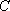
(2)当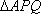
正确答案
(1)
(2)
解析
(1)将圆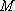
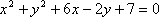
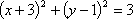
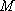
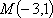
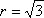
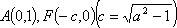
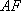
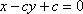
由直线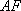
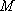
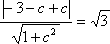
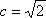
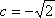
当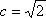
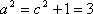
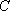
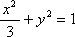
(2)由题意可知,直线的斜率存在,设直线的斜率为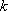
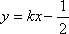
因为点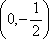
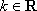
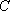
由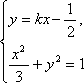
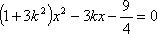
设点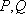
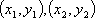
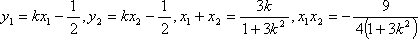
所以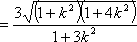
又因为点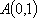
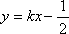
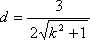
所以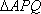
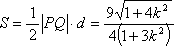
设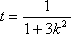
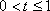
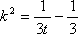
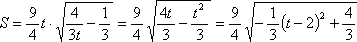
因为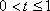
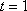
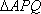
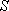
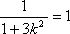
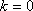
故当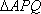
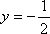
知识点
已知椭圆








正确答案
解析
过点B作





知识点
已知椭圆








(1)证明:椭圆上的点到

(2)求椭圆的离心率
(3)设椭圆的短半轴长为











正确答案
见解析
解析
解析:
(1)设椭圆上任一点









(2)依题意设切线长
∴当且仅当



从而解得


(3)依题意


得







(11分)










知识点
已知椭圆C:


(1)求椭圆C的方程;
(2)记椭圆C的上顶点为B,直线l交椭圆C于P,Q两点,问:是否存在直线l,使椭圆C的右焦点F2恰为△PQB的垂心(△PQB三条边上的高线的交点)?若存在,求出直线l的方程,若不存在,请说明理由。
(3)若⊙M是以AF2为直径的圆,求证:⊙M与以坐标原点为圆心,a为半径的圆相内切。
正确答案
见解析。
解析
(1)∵椭圆C:

∴
该椭圆上一点A与左、右焦点F1,F2构成的三角形周长为2
∴|AF1|+|AF2|+|F1F2|=2a+2c=
解得a=

∴椭圆C的方程为
(2)假设存在直线l,使椭圆C的右焦点F2恰为△PQB的垂心。
设P(x1,y1),Q(x2,y2),则BF2⊥PQ。
∵B(0,1),F2(1,0),∴
设直线l的方程为:y=x+m,联立
化为3x2+4mx+2m2﹣2=0,则x1+x2=

∵
∴x1(x2﹣1)+y2(y1﹣1)=0,
∴x1(x2﹣1)+(x2+m)(x1+m﹣1)=0,化为2x1x2+(x1+x2)(m﹣1)+m2﹣m=0,
∴


经检验m=﹣

(3)证明:设A(x0,y0),F2(1,0),则M
设两圆的半径分别为r1,r2。
|OM|=


又⊙M的半径r1=|MF2|=

∴r2﹣r1=

∴|OM|=r2﹣r1。
∴⊙M与以坐标原点为圆心,a为半径的圆相内切。
知识点
离心率为



正确答案
解析
解析:
设椭圆



















知识点
扫码查看完整答案与解析