- 向量的线性运算性质及几何意义
- 共16题
1
题型:填空题
|
5. 已知点A分有向线段


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
向量的线性运算性质及几何意义平面向量的坐标运算
1
题型:
单选题
|
17. 如图,一质点

















正确答案
D
解析
探究


知识点
向量的线性运算性质及几何意义数列与向量的综合
1
题型:
单选题
|
12.已知双曲线



则下列各式成立的是( )
正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
向量的线性运算性质及几何意义向量在几何中的应用双曲线的几何性质
1
题型:填空题
|
16.设
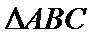
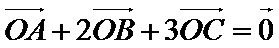
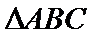
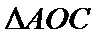
正确答案
3
解析
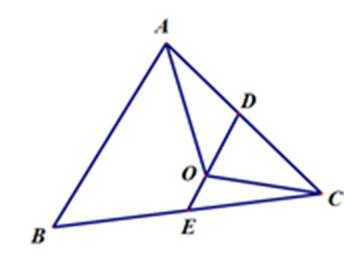
如图,
设D、E分别是AC、BC的中点,则: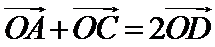
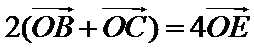
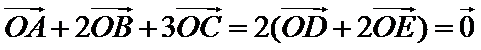
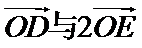
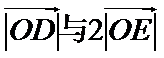
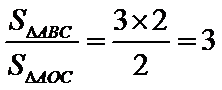
考查方向
本题主要考查了平面向量的运算问题,同时考查了转化与化归的数学思想方法。
解题思路
通过添加辅助线,再根据题目中给出的关系可已确定图形中的一些数量关系,进而即可求解。
易错点
本题容易因为不能准确地对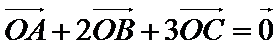
知识点
向量的线性运算性质及几何意义
1
题型:填空题
|
15.定义在区间










正确答案
解析
由题意可知
∴
又因为
∴
所以
考查方向
本题主要考察了平面向量的坐标运算,考察了平面向量共线(平行)的坐标表示,考察了向量的减法运算,考察了二次函数在闭区间上的最值,考察了绝对值不等式的解法,考察了函数恒成立问题,该题信息量较大,变量较多,属于题型中的中档题
解题思路
1、根据题意给定区间,把



易错点
本题易错于因为信息量大,数据处理不全,找不到解题思路
知识点
向量的线性运算性质及几何意义
下一知识点 : 平面向量的基本定理及其意义
扫码查看完整答案与解析