- 正弦定理
- 共139题
在
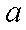
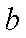

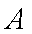
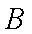
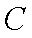

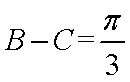
(1) 求角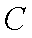
(2) 若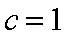
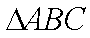
正确答案
见解析
解析
(1)由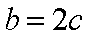
又由正弦定理,得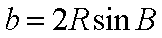
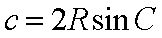
将其代入上式,得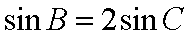
∵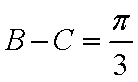
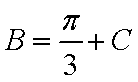
∴
整理得,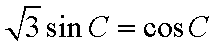
∴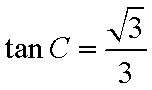
∵角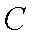
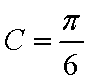
(2) ∵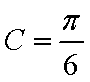
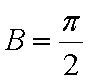
又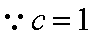
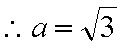
∴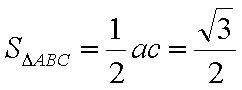
知识点
已知


(1)若
(2)若


正确答案
(1)
解析
(1)



(2)由

由余弦定理可知:
于是ab =4...................10分

知识点
在







正确答案
解析
略
知识点


正确答案
解析
由正弦定理可将








知识点
已知函数

(1)求常数
(2)在











正确答案
见解析
解析
(1)

∵ 

∵ 函数


∴当



此时,

(2)∵ 

∴


∵


∵ 

∴ 

由①和②解得

∴ 
知识点
扫码查看完整答案与解析