- 函数概念与表示
- 共1891题
已知函数
(1)若函数





(2)若



正确答案
见解析。
解析
(1)已知函数
又函数







令
所以函数的单调递减区间为
(2)当





即


知识点
函数








正确答案
见解析。
解析

依题意有 
即

令









知识点
某地建一座桥,两端的桥墩已建好,这两墩相距



(1)试写出

(2)当

正确答案
见解析。
解析
(1)设需要新建
所以
(2) 由(1)知,
令


当0<


当


所以

故需新建9个桥墩才能使
知识点
已知函数
(1)当

(2)若函数
正确答案
见解析。
解析
(1)函数
当

当

……………………………………………………5分



(2)由

又函数
在[1,4]上恒成立,所以不等式
即
设

所以



知识点
已知函数
(1)当


(2)如果函数

那么就称




函数


正确答案
见解析。
解析
(1)当

对于



∴
(2)在区间





且

∵
①若






此时



②若



从而

要使


又因为



综合可知

另解:(接在(*)号后)
先考虑






而



只要



即

知识点
已知直线



(1)求直线

(2)若

正确答案
见解析。
解析
(1)
又因为直线
(2)由(1)知
当
于是,
所以,当
知识点
已知直线



(1)求直线

(2)若

正确答案
见解析。
解析
(1)
又因为直线
(2)由(1)知
当
于是,
所以,当
知识点
设函数


(1)求

(2)若函数在

正确答案
见解析。
解析
(1)



∵切线


把


∴
∴

(2)由(1)
由已知得:
∴
∴
∴
由

由

∴

单调减区间为
知识点
已知函数f (x)=
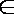
(1)曲线C:y=f (x) 经过点P (1,2),且曲线C在点P处的切线平行于直线y=2x+1,求a,b的值;
(2) 已知f (x)在区间 (1,2) 内存在两个极值点,求证:0<a+b<2。
正确答案
见解析。
解析
(1)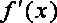
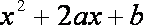
由题设知: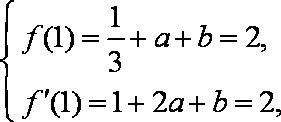
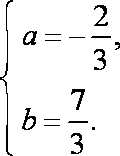
(2)解:因为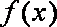
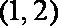
所以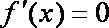
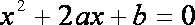
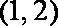
故
由 (1)+(3)得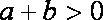
由(4)得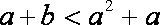
因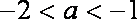
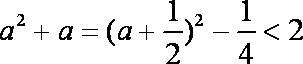
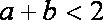
所以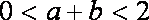
知识点
已知函数f(x)=x3-ax2-3x.
(1)若f(x)在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=-是f(x)的极值点,求f(x)在[1,a]上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数g(x)=bx的图象与函数f(x)的图象恰有3个交点?若存在,请求出实数b的取值范围;若不存在,试说明理由。
正确答案
见解析。
解析
(1)f′(x)=3x2-2ax-3.
∵f(x)在[1,+∞)是增函数,
∴f′(x)在[1,+∞)上恒有f′(x)≥0,即
3x2-2ax-3≥0在[1,+∞)上恒成立,
则必有≤1且f′(1)=-2a≥0.∴a≤0. ………4分
(2)依题意,f′(-)=0,
即+a-3=0.
∴a=4,∴f(x)=x3-4x2-3x.
令f′(x)=3x2-8x-3=0,
得x1=-,x2=3.
则当x变化时,f′(x)与f(x)变化情况如下表
∴f(x)在[1,4]上的最大值是f(1)=-6. ………8分
(3)函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,即方程x3-4x2-3x=bx恰有3个不等实根。
∴x3-4x2-3x-bx=0,
∴x=0是其中一个根,
∴方程x2-4x-3-b=0有两个非零不等实根。
∴
∴b>-7且b≠-3.
∴存在满足条件的b值,b的取值范围是b>-7且b≠-3. ………12分
知识点
扫码查看完整答案与解析