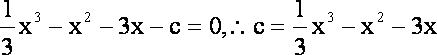- 函数概念与表示
- 共1891题
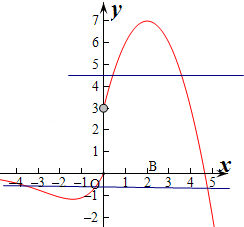
设函数

(1)求a,b的值;
(2)证明:
正确答案
见解析。
解析
(1)
由已知条件得
(2)
设
而
知识点
已知函数f(x)=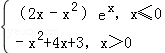
正确答案
(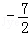
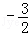
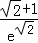
解析
由g(x)=f(x)+2k=0,即f(x)=﹣2k,
当x≤0时,f(x)=(2x﹣x2)ex,
则f'(x)=(2﹣x2)ex,由f'(x)=(2﹣x2)ex=0,解得x=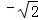
当x=﹣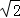
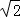
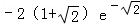
当x>0时,f(x)=﹣x2+4x+3=﹣(x﹣2)2+7≤7,
作出函数f(x)的图象,由图象可知,要使f(x)=﹣2k有恰有两个不同的交点,
则满足3<﹣2k<7,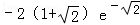
即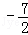
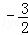
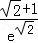
当k=0时,f(x)=﹣2k,有两个交点,满足条件。
知识点
设函数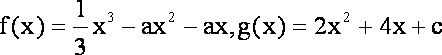
(1) 试问函数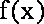

(2) 若a=-1,当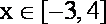
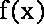
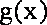
正确答案
见解析。
解析
(1)由题意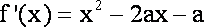
假设在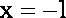
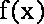
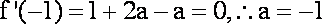
而此时,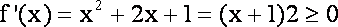
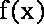
这与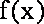
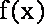
(2)设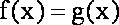
设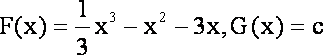
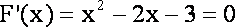
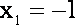

列表如下:
由此可知:F(x)在(-3,-1)、(3,4)上是增函数,在(-1,3)上是减函数。……10分
当x=-1时,F(x)取得极大值F(-1)=
F(-3)=F(3)=-9,而F(4)=-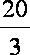
如果函数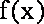
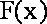
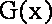
所以
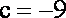
知识点
已知函数
(1)当a=1时,求函数f(x)的极值;
(2)若函数f(x)在区间(0,1)上是单调增函数,求实数a的取值范围。
正确答案
见解析。
解析
(1)因为

令

所以x=0时,f(x)取得极小值f(0)=-1.
(2)因为





解法一:设


只要


解法二:要使




因为函数
知识点
已知函数
(1)求函数
(2)若函数


问: 



正确答案
见解析。
解析
(1)由
当



当



(2)由
∴

∴
∵ 函数

∴

又∵函数


由


所以



综上得:





知识点
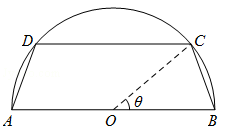
一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分,现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设∠BOC=θ,木梁的体积为V(单位:m3),表面积为S(单位:m2)。
(1)求V关于θ的函数表达式;
(2)求θ的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由。
正确答案
见解析。
解析
(1)梯形ABCD的面积S=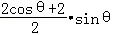
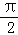
体积V(θ)=10(sinθcosθ+sinθ),θ∈(0,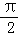
(2)V′(θ)=10(2cos2θ+cosθ﹣1)=10(2cosθ﹣1)(cosθ+1)。
令V′(θ)=0,得cosθ=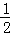
∵θ∈(0,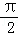
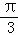
当θ∈(0,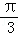
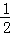
当θ∈(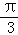
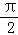
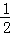
∴当θ=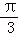
(3)木梁的侧面积S侧=10(AB+2BC+CD)=20(cosθ+2sin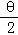
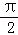
∴表面积S=2(siθcosθ+sinθ)+20(cosθ+2sin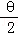

设g(θ)=cosθ+2sin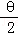
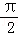
∵g(θ)=﹣2sin2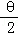
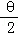
∴当sin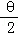
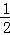
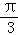
又由(2)知θ=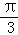
∴θ=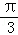
综上,当木梁的体积V最大时,其表面积S也最大。
知识点
函数
正确答案
解析
令




知识点
已知函数f(x)=mx﹣αlnx﹣m,g(x)=
(1)求g(x)的极值;
(2)设m=1,α<0,若对任意的x1,x2∈[3,4](x1≠x2),|f(x2)﹣f(x1)|<|

(3)设α=2,若对任意给定的x0∈(0,e],在区间(0,e]上总存在t1、t2(t1≠t2),使得f(t1)=f(t2)=g(x0)成立,求m的取值范围。
正确答案
见解析。
解析
(1)g′(x)=

∵ex>0,∴x∈(﹣∞,1)时,g′(x)>0;x∈(1,+∞)时,g′(x)<0,根据极大值的定义知:g(x)极大值是g(1)=1,无极小值。
(2)当m=1,a<0时,f(x)=x﹣alnx﹣1,所以在[3,4]上f′(x)=
设h(x)=

设x2>x1,则


∴u′(x)=1﹣
∴




∴v(x)在[3,4]上的最大值为v(3)=
∴a≥

(3)由(1)知g(x)在(0,1]上单调递增,在(1,e]单调单调递减,又g(0)=0,g(e)=
∵f(x)=mx﹣2lnx﹣m;
∴当m=0时,f(x)=﹣2lnx,在(0,e]为减函数,由题意知,f(x)在(0,e]不是单调函数;故m=0不合题意;
当m≠0时,f′(x)=


此时f(x)在(0,

∴f(e)≥1,即me﹣2﹣m≥1,解得
所以由①②,得
∵1∈(0,e],∴f(
下证存在t∈(0,
取t=e﹣m,先证
设w(x)=2ex﹣x,则w′(x)=2ex﹣1>0在[
∴w(x)在[

再证f(e﹣m)≥1;
∵f

所以m的取值范围是:[
知识点
已知函数


正确答案
解析
依题意,设

又




知识点
已知函数
(1)求函数
(2)若

正确答案
见解析。
解析
(1)
增区间为
(2)




知识点
扫码查看完整答案与解析