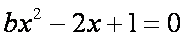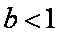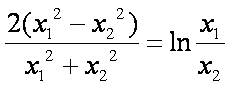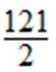- 函数概念与表示
- 共1891题
记定义在


(1)当

(2)直接写出
(3)在所有形如题设的函数


正确答案
见解析。
解析
(1)当


所以
此时,
(2)由(1)同理可得,
(3)记



①若


所以

②若





所以




所以


由



综上所述,所有形如题设的函数
知识点
已知函数f(x)=lnx﹣ax2﹣x,a∈R。
(1)若函数y=f(x)在其定义域内是单调增函数,求a的取值范围;
(2)设函数y=f(x)的图象被点P(2,f(2))分成的两部分为c1,c2(点P除外),该函数图象在点P处的切线为l,且c1,c2分别完全位于直线l的两侧,试求所有满足条件的a的值。
正确答案
见解析
解析
解:(1)
只需要2ax2+x﹣1≤0,即
所以
(2)因为
所以切线l的方程为
令

若a=0,则
当x∈(0,2)时,g'(x)>0;当x∈(2,+∞)时,g'(x)<0,
所以g(x)≥g(2)=0,c1,c2在直线l同侧,不合题意;
若a≠0,
若

当x∈(2,+∞)时,g(x)>g(2)=0;当x∈(0,2)时,g(x)<g(2)=0,符合题意;
若

当x∈(2,+∞)时,g'(x)>0,g(x)>g(2)=0,不合题意;
若

当x∈(0,2)时,g'(x)>0,g(x)<g(2)=0,不合题意;
若a>0,当x∈(0,2)时,g'(x)>0,g(x)<g(2)=0,
当x∈(2.+∞)时,g'(x)<0,g(x)<g(2)=0,不合题意。
故只有
知识点
已知(其中



(1)试求
(2)先列表再作出函数

正确答案
见解析
解析
解析: 由题设得

=
(1)


∴

∴

(2)由(1)知
列表如下

则函数

(12分)
知识点
函数
(1)当x>0时,求证:
(2)是否存在实数a使得在区间(1.2)上
(3)当

正确答案
见解析
解析
(1)明:设
则




(2)由

当


当


另


因为




所以

(3)由第一问得知

则
又


知识点
已知函数
正确答案
解析
解:∵ f(x)=
由图可知,当a=1时,直线y=



∴ bf(a)=


当b=1时,直线y=3与f(x)只有一个交点,且f(a)=f(b)=3,
∴ bf(a)=1×3=3,
∴ bf(a)的取值范围为[
知识点
甲、乙两大超市同时开业,第一年的全年销售额均为




(1)求甲、乙两超市第
(2)若其中某一超市的年销售额不足另一超市的年销售额的50%,则该超市将被另一超市收购,判断哪一超市有可能被收购?如果有这种情况,将会出现在第几年?
正确答案
见解析
解析
解析:(1)设甲超市第






则

.........................................................................................................................................3分
故
设乙超市第




显然

(2)当




当


当

则
又当

故当


即第7年乙超市的年销售额不足甲超市的一半,乙超市将被甲超市收购。 13分
知识点
已知函数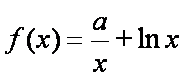
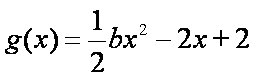

(1)求函数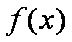
(2)记函数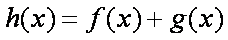
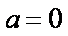

(3)记函数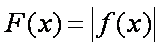
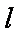
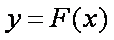
正确答案
见解析
解析
(1)因为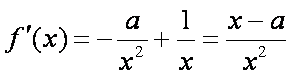
①若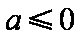
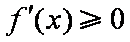
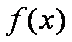
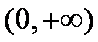
②若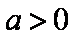
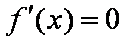
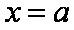
当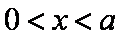
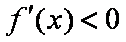
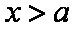
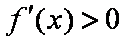
所以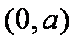
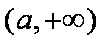
综上可得,当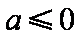
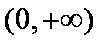
当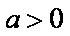
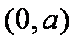
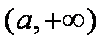
(2)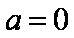
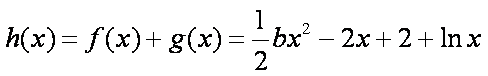
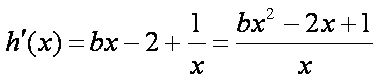
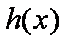
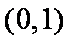
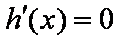
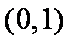
由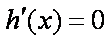
(i)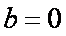
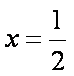
(ii)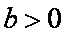
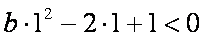
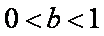
(iii)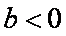
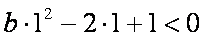
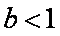
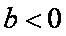
综上得: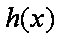
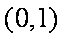
注:本题也可分离变量求得。
(3)证明:由(1)可知:
(i)若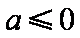
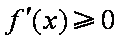
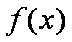
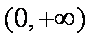
所以直线
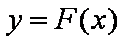
(ⅱ)若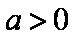
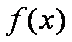
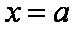
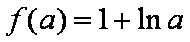
若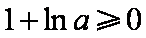

故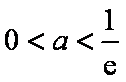
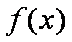
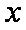
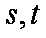
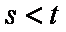
则直线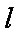
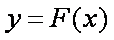
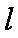
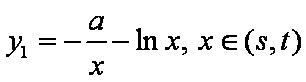
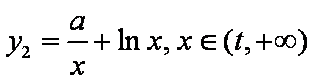
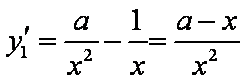
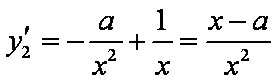
设切点分别为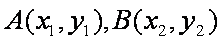

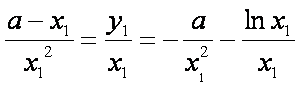
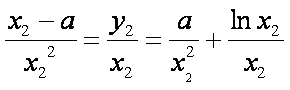
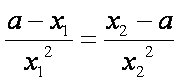
即

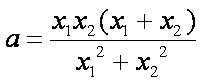
①-②得: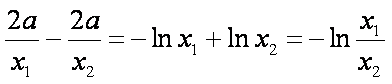
由③中的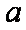
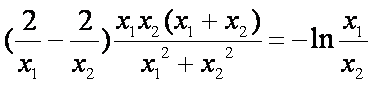
即
令
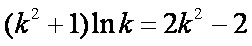
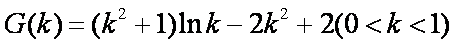
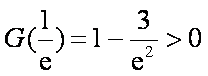
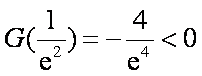
故存在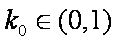
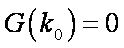
即存在一条过原点的直线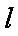
知识点
正确答案
解析
知识点
已知关于
(1)设集合







(2)设点





正确答案
见解析。
解析
(1)∵函数
要使

当且仅当

若





记


则事件


(2)依条件可知试验的全部结果所构成的区域为
其面积
事件
由




知识点
已知

①

正确答案
①③④
解析
因为











知识点
扫码查看完整答案与解析