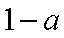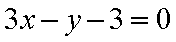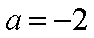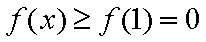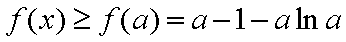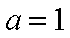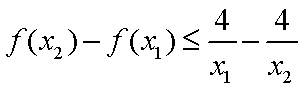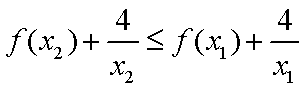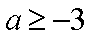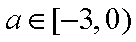- 函数概念与表示
- 共1891题
函数










正确答案
解析
由于





知识点
已知点P在半径为1的半圆周上沿着A



①函数

②如果函数

③如果函数

④函数

以上结论的正确个数是( )
正确答案
解析
因为









知识点
近年来,某企业每年消耗电费约24万元, 为了节能减排, 决定安装一个可使用15年的太阳能供电设备接入本企业电网, 安装这种供电设备的工本费(单位: 万元)与太阳能电池板的面积(单位: 平方米)成正比, 比例系数约为0.5. 为了保证正常用电, 安装后采用太阳能和电能互补供电的模式. 假设在此模式下, 安装后该企业每年消耗的电费



(1)试解释


(2)当

正确答案
见解析
解析
解: (1) 
即未安装电阳能供电设备时全村每年消耗的电费
由

所以
(2)因为
当且仅当

所以当

知识点
对于定义在区间





(1) 试判断

(2) 若函数


(3)若函数


正确答案
见解析
解析
解: (1)


而[-1,0]


(2)因为
①当


②当



由


③当


综上所述, 实数
(3)因为

所以



①当



②当

③当


又


④当



而
⑤当

⑥当



综上所述,所求整数
知识点
已知函数


(1)求
(2)若

正确答案
见解析
解析
(1)由函数的周期为

又由

又
(2)(方法一)由
因为
又

所以
(方法二)由
因为
又

所以
所以
知识点
已知


则
正确答案


解析
构造新函数

有




所以,












知识点
为了解某校教师使用多媒体进行教学的情况,采用简单随机抽样的方法,从该校200名授课教师中抽取20名教师,调查了他们上学期使用多媒体进行教学的次数,结果用茎叶图表示如下:
据此可估计该校上学期200名教师中,使用多媒体
进行教学次数在
正确答案
100
解析
所抽取的20人中在
故可得200名教师中使用多媒体进行教学次数在

知识点
设函数




(1)求证:
(2)试问:在

(3)解关于
正确答案
见解析
解析
解析:(1)设


所以
(2)任取

所以
所以
那么函数最大值为

所以函数最大值为4,所以函数最小值为-4,
(3)由题设可知
即
可化为
即


所以解为
知识点
已知函数
(1)若曲线


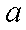
(2)求证:
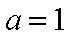
(3)若
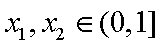
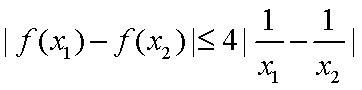

正确答案
见解析
解析
(1)因为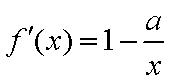

所以曲线
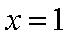
因为曲线

所以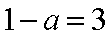
(2)①充分性。
当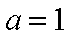
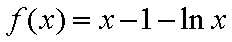
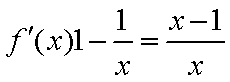
所以当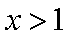

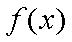

当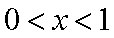
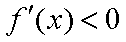


所以
②必要性。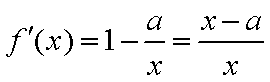

(i)当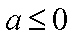
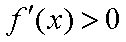

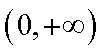
而

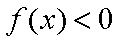

所以
(ii)当
因为当



当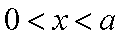



所以
因为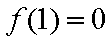
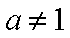

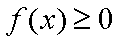
所以
综上所述,
(3)由(2)可知,
当

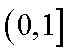

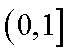
不妨设
则
所以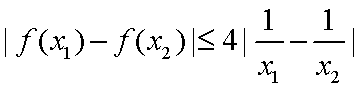
即
设
则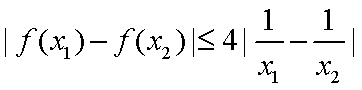

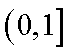
因为

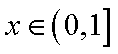
即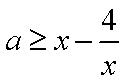
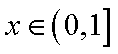


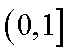
而函数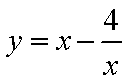
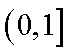
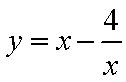
所以
又
知识点
若直角坐标平面内两点P、Q满足条件:
①P、Q都在函数
②P、Q关于原点对称,则称点对(P,Q)是函数
已知函数

正确答案
2
解析
由题意,在函数





令
由图像可知:
知识点
扫码查看完整答案与解析