- 函数概念与表示
- 共1891题
已知数列{an}满足:a1=a2=a3=2,an+1=a1a2…an-1(n≥3),记

(1)求证数列{bn}为等差数列,并求其通项公式;
(2)设

正确答案
见解析。
解析
(1)方法一 当n≥3时,因
故
②-①,得 bn-1-bn-2=

所以,数列{bn}为等差数列,
因 b1=
方法二 当n≥3时,a1a2…an=1+an+1,a1a2…anan+1=1+an+2,
将上两式相除并变形,得 
于是,当n∈N*时,

又a4=a1a2a3-1=7,故bn=n+3(n∈N*)。
所以数列{bn}为等差数列,且bn=n+3.
(2) 方法一 因 
故 
所以 
即 n<Sn<n+1.
方法二 因


=


故


第(2)问,为了结果的美观,将Sn放缩范围放得较宽,并且可以改为求不小于Sn的最小正整数或求不大于Sn的最大正整数。
本题(2)的方法二是错误的,请不要采用。
注意
=


故


于是
知识点
设函数f(x)=ax3-(a+b)x2+bx+c,其中a>0,b,c∈R。
(1)若
(2)求证:当0≤x≤1时,|

正确答案
见解析。
解析
(1)由
故f(x)= ax3-2ax2+ax+c。
由

列表:
由表可得,函数f(x)的单调增区间是(-∞,
(2)

①当


所以







所以|

②当



(i)当-a<b≤

所以 



所以 |

(ii)当


所以




所以 |

综上所述:当0≤x≤1时,|
知识点
若函数


则实数
正确答案
-5或-1
解析
由

故当





知识点
若函数
(1)当





(i)求证:

(ii)求证:
(2)当



正确答案
见解析。
解析
(1)(i)因为
所以









(ii)设x1,x2是方程




分别比较(*)式中常数项和含x3的项的系数,得

解得

所以
分别比较①式中含x和x2的项的系数,得


②×


(2)方程化为:
令


设
当



当



当








知识点
对于定义在R上的函数f(x),给出三个命题:
①若
②若
③若
其中正确命题的序号为 ▲ 。
正确答案
②
解析
命题③学生很容易判为真命题。
反例:函数

请注意以下问题:既是奇函数又是偶函数的函数是否唯一?
命题是否定的,如函数


知识点
如图,函数y=f(x)的图象是中心在原点、焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(﹣x)+x的解集为( )
正确答案
解析
解:由图象知f(x)为奇函数,∴f(﹣x)=﹣f(x)。
∴原不等式可化为f(x)<

与直线y=


∴x2=2,x=±
观察图象知:﹣

知识点
已知二次函数




(1)求
(2) 若曲线


(3) 若

正确答案
见解析
解析
(1)设

∴

∴
∵
∴
∴
(2)
∵
∴
∵

由题意得
∴
∴

(3)∵
∴
令
∴
∴
∴
∵
①
②

③

知识点
已知三次函数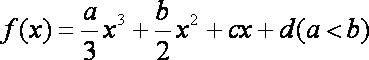
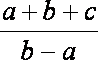
值为 ▲ 。
正确答案
3
解析
由题意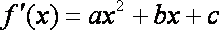
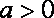
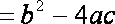
∴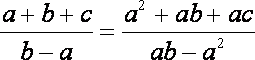
令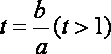
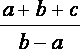
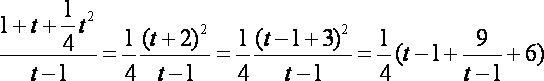
(当且仅当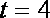
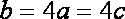
知识点
定义在
正确答案
1或2
解析
由已知可得:当

当



由题意点


知识点
设函数f(x)=ax3﹣2bx2+cx+4d(a、b、c、d∈R)图象关于原点对称,且x=1时,f(x)取极小值
(1)求a、b、c、d的值;
(2)当x∈[﹣1,1]时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;
(3)若x1,x2∈[﹣1,1]时,求证:
正确答案
见解析
解析
解(1)∵函数f(x)图象关于原点对称,∴对任意实数x有f(﹣x)=﹣f(x),
∴﹣ax3﹣2bx2﹣cx+4d=﹣ax3+2bx2﹣cx﹣4d,即bx2﹣2d=0恒成立,
∴b=0,d=0,∴f(x)=ax3+cx,f'(x)=3ax2+c,
∵x=1时,f(x)取极小值


解得
故
(2)当x∈[﹣1,1]时,图象上不存在这样的两点使结论成立。
假设图象上存在两点A(x1,y1)、B(x2,y2),使得过此两点处的切线互相垂直,
则由f'(x)=x2﹣1,知两点处的切线斜率分别为
且
∵x1、x2∈[﹣1,1],∴
此与(*)相矛盾,故假设不成立。
(3)证明:∵f'(x)=x2﹣1,令f'(x)=0,得x=±1,
∵x∈(﹣∞,﹣1),或x∈(1,+∞)时,f'(x)>0;x∈(﹣1,1)时,f'(x)<0,
∴f(x)在[﹣1,1]上是减函数,且
∴在[﹣1,1]上,

知识点
扫码查看完整答案与解析