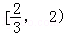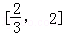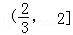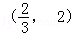- 函数概念与表示
- 共1891题
已知函数f(x)=sin(4x+

(1)求函数f(x)的最大值;
(2)若直线x=m是曲线y=f(x)的对称轴,求实数m的值。
正确答案
(1)2(2)
解析
解析:(1)

所以
(2)令
则
而直线


知识点
已知函数
(1)当a=2时,求函数y=f(x)的单调区间;
(2)当a>0时,函数y=f(x)在闭区间

正确答案
见解析
解析
f/(x)=6x2-6(a+1)x+6a
=6(x-1)(x-a)……………2分
(1)当a=2时,f/(x)=6(x-1)(x-a)= 6(x-1)(x-2)
当x<1或x>2时,f/(x)>0,
当1<x<2,f/(x)<0,
所以f(x)的单调增区间分别为(-∞,1),(2,+∞),………………5分
f(x)的单调减区间为(1,2)
(2)(Ⅰ)当a=1时,f/(x)=6(x-1)2≥0,f(x)在 [0,a+1]上单调递增,最大值为f(a+1)
(Ⅱ)当0<a<1时,列表如下:
由表知f(x)在[0,a+1]上的最大值,只有可能是f(a)或 f(a+1)
所以只需f(a+1) -f(a)=(-a3+3a2+3a-1)-(-a3+3a2)=3a-1≥0
解得a≥

(Ⅲ)当a>1时,列表如下:
由表知f(x)在[0,a+1]上的最大值,只有可能是f(1)或 f(a+1)
所以只需f(a+1) -f(1)=(-a3+3a2+3a-1)-(3a-1)=- a 3+3a2=-a2(a-3)≥0
解得a≤3,此时1<a≤3.………………11分
由(Ⅰ)(Ⅱ)(Ⅲ)得
所以满足条件的a的取值范围是[
知识点
已知函数f(x)=loga(2x+b﹣1)(a>0,且a≠1)在R上单调递增,且2a+b≤4,则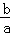
正确答案
解析
已知函数f(x)=loga(2x+b﹣1)(a>0,且a≠1)在R上单调递增,
而函数t=2x+b﹣1是R上的增函数,故有a>1。
再根据t>0恒成立可得b≥1。
又2a+b≤4,∴1≤b<2,∴2a≤3,
∴1<a≤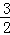
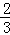
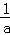
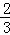
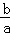
则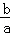

知识点
以直角坐标系的原点








(1)求直线

(2)试判定直线



正确答案
(1)
(2)相交,
解析
(1)因为直线


所以直线

如图,设圆上任意一点为

得
∴
化简得



因为

即圆

(2)因为圆心M的直角坐标是

所以直线l和圆



知识点
已知2013年2月10日春节,某蔬菜基地2013年2月2日有一批黄瓜进入市场销售,通过市场调查,预测黄瓜的价格



(1)根据上表数据,从下列函数中选取一个函数描述黄瓜价格





(2)为了控制黄瓜的价格,不使黄瓜的价格过于偏高,经过市场调研,引入一控制函数

求证:当


正确答案
见解析。
解析
(1)根据表中数据,表述黄瓜价格










所以,黄瓜价格


(2)设函数



表格如下: ……8分
由上表可知









于是有


故







即
知识点
已知函数
(1)函数


(2)设

正确答案
(1)b=
解析
(1)因为


即函数
∴函数
由

解得
(2)因为
所以
由题意知

因为x>0,设

所以只要
从而解得b>2,所以b的取值范围为
知识点
设
(1)若

(2)若函数
正确答案
(1)a=1(2)
解析
(1)
因为


即

经验证,当



(2)由题设知,
当





反之,当


而



综上,

知识点
函数f(x)=x2﹣ax+1在区间
正确答案
解析
由f(x)=x2﹣ax+1在区间
可得x2﹣ax+1=0在区间
∴
化解


化解


综上a∈
知识点
函数f(x)=ln
正确答案
(﹣∞,0]
解析
∵|x|≥0,∴|x|+1≥1,
从而
再根据对数函数的单调性,有

故所求值域为(﹣∞,0]。
知识点
函数f(x)=
正确答案
解析
函数f(x)=

令2x+



故函数的一条对称轴方程为x=


知识点
扫码查看完整答案与解析