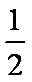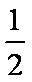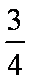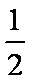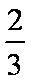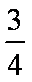- 函数概念与表示
- 共1891题
已知函数
(1)当

(2)若

正确答案
(1)
解析
解析:(1)当

①当



②当



③当



综上原不等式的解集为
(2)
不等式可化为
解得
由已知得
解得
所以

知识点
在函数①y= sin|2x|,②y=l-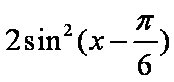
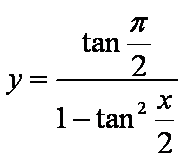
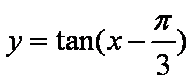
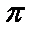
正确答案
解析
略
知识点
已知△ABC中,a,b,c分别为∠A,∠B,∠C的对边,∠B=60°,b=2,a=x,如c有两组解,则x的取值范围是 。
正确答案
解析
当asinB<b<a时,三角形ABC有两组解,
又b=2,B=60°,a=x,如果三角形ABC有两组解,
那么x应满足xsin60°<2<x,
即。
x的取值范围是:
知识点
已知点A(a,1)和曲线C:x2+y2﹣x﹣y=0,若过点A的任意直线都与曲线C至少有一个交点,则实数a的取值范围是 。
正确答案
[0,1]
解析
∵圆的标准方程为(x﹣


∴圆心坐标为(


当y=1时,方程x2+y2﹣x﹣y=0为x2+1﹣x﹣1=0,
即x2﹣x=0,
解得:x=0或x=1,
要使过点A的任意直线都与曲线C至少有一个交点,
则点A应该在圆上或者在圆内,
则a满足0≤a≤1,
知识点
已知函数f(x)=(a+1)x2﹣2ax﹣2lnx。
(1)求证:a=0时,f(x)≥1恒成立;
(2)当a∈[﹣2,﹣1]时,求f(x)的单调区间。
正确答案
见解析。
解析
(1)a=0时,f(x)=x2﹣2lnx,x∈(0,+∞),

令f'(x)=0,
解得:x=1,x=﹣1(舍去)
当x∈(0,1)时,f'(x)<0,f(x)在(0,1)上单调递减;
当x∈(1,+∞)时,f'(x)>0,f(x)在(1,+∞)上单调递增。
∴f(x)min=f(x)极小值=f(1)=1
所以,∀x∈(0,+∞),f(x)≥1.
(2)f(x)的定义域为(0,+∞),
①当a=﹣1时,
此时f(x)在区间(1,+∞)上单调递增,在(0,1)上单调递减;
②当a<﹣1时,
令f'(x)=0,解得:
(i)当﹣2<a<﹣1时,
令f'(x)>0,解得:
令f'(x)<0,解得:
此时f(x)在区间

(ii)当a=﹣2时,
此时
综上,a=﹣1时,f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1);
﹣2<a<﹣1时,f(x)的单调递增区间为

a=﹣2时,f(x)的单调递减区间为(0,+∞),无单调增区间。
知识点
已知函数

正确答案
解析
略
知识点
已知函数f(x)=x+
(1)求切线ln的方程及数列{an}的通项;
(2)设数列{nan}的前n项和为Sn,求证:Sn<1。
正确答案
见解析。
解析
(1)对

则切线ln方程为:

把x=n+1分别代入

得

由an=|AnBn|知,

(2)证明:∵nan=


∴Sn=1•a1+2•a2+…+n•an
=

知识点
已知函数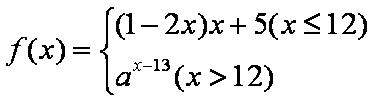
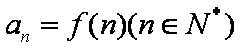
正确答案
解析
略
知识点
若函数



正确答案
解析
略
知识点
已知函数

(1)求
(2)若

正确答案
(1)
解析
解析:(1)依题意

经检验,
(2)由(Ⅰ)知

令


方程


则


且当



所以当




则

得
又令







知识点
扫码查看完整答案与解析