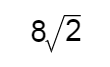点与圆的位置关系
共46题

· 点与圆的位置关系

点与圆的位置关系
共46题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

21．已知，，（，）．函数定义为：对每个给定的实数，

（1）若对所有实数都成立，求的取值范围；

（2）设．当时，若对任意，存在，使得，求实数的取值范围

正确答案

（1）“对所有实数都成立”等价于“恒成立”，

，即恒成立，

，所以，

的取值范围是．

（2）当时，

对任意，存在，使得，

，

，当时，，

由或或，

解析

解析已在路上飞奔，马上就到！

知识点

点与圆的位置关系

题型：填空题

填空题 · 5 分

以直角坐标系的原点为极点，x轴的正半轴为极轴，并在两种坐标系中取相同的长度单位，已知直线的极坐标方程为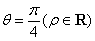，它与曲线为参数）相交于A和B两点，则= 。

正确答案

解析

略

知识点

点与圆的位置关系

题型：填空题

填空题 · 5 分

一只艘船以均匀的速度由A点向正北方向航行，如图，开始航行时，从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°，行驶60海里后，船在B点观测灯塔C的方位角为75°，则A到C的距离是__________海里。

正确答案

解析

,中，由正弦定理，

知识点

点与圆的位置关系

题型：单选题

单选题 · 5 分

已知集合，，若，则实数所有可能取值的集合为（）

正确答案

解析

时，，时，，，故选或或-1，选D。

知识点

点与圆的位置关系

题型：单选题

单选题 · 5 分

已知函数在［0，］恰有4个零点，则正整数的值为.

A2或3

B3或4

C4或5

D5或6

正确答案

解析

略

知识点

点与圆的位置关系

题型：简答题

简答题 · 14 分

在四棱柱中，底面，底面为菱形，为与交点，已知,.

（1）求证：平面；

（2）求证：∥平面；

（3）设点在内（含边界）,且，说明满足条件的点的轨迹，并求的最小值。

正确答案

见解析

解析

（1）依题意, 因为四棱柱中，底面，

所以底面.

又底面,

所以.

因为为菱形，

所以.而，

所以平面. ………………4分

（2）连接,交于点，连接.

依题意，∥,

且，,

所以为矩形。

所以∥.

又,,,

所以=，所以为平行四边形，

则∥.

又平面，平面,

所以∥平面. ……………………………………………………………9分

（3）在内，满足的点的轨迹是线段，包括端点。

如下：连接，则.

由于∥,故欲使，只需,从而需.

又在中，,又为中点，所以.

故点一定在线段上。

当时，取最小值。

在直角三角形中，,,,

所以. …………………………………………………………………14分

知识点

点与圆的位置关系

题型：单选题

单选题 · 5 分

设两圆C1、C2都和两坐标轴相切，且都过点(4,1)，则两圆心的距离|C1C2|＝(　　)

正确答案

解析

知识点

点与圆的位置关系

题型：单选题

单选题 · 5 分

已知圆与抛物线的准线相切，则m=

A±2

D±

正确答案

解析

略

知识点

点与圆的位置关系

题型：填空题

填空题 · 5 分

如果是函数图像上的点，是函数图像上的点，且两点之间的距离能取到最小值，那么将称为函数与之间的距离.按这个定义，函数和之间的距离是 .

正确答案

解析

略

知识点

点与圆的位置关系

题型：填空题

填空题 · 4 分

若直线过点，且与圆相切，则直线的方程为　　　　　。

正确答案

或；

解析

略

知识点

点与圆的位置关系

继续学习学习下一知识点

下一知识点 : 关于点、直线对称的圆的方程

百度题库 > 高考 > 文科数学 > 点与圆的位置关系

扫码查看完整答案与解析