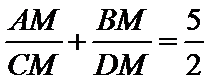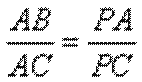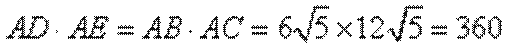- 点与圆的位置关系
- 共46题
21. 如图,已知点











(1)求椭圆
(2)求证:直线

正确答案
(1)由题意,可得



解得


所以椭圆

(2)证明:设直线





由
所以


设直线



则

将①、②式代入(*),
整理得
所以


解析
解析已在路上飞奔,马上就到!
知识点
14.若圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如图,在正方体ABCD-A1B1C1D1中,EF=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
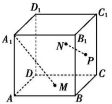
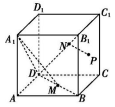
8.如图,M,N,P分别是正方体ABCD-A1B1C1D1的三个侧面ABCD,CC1D1D,BCC1B1的中心,则A1M与NP所成角的大小是( )
正确答案
解析
知识点
5.若在区间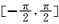
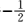
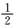
正确答案
解析
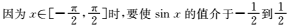
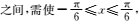
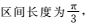

知识点
9.若对于正数x,y满足
正确答案
解析




知识点
4.若a,b为不相等的正数,且x= 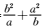
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.抛物线y=x2与直线x-y+2=0构成封闭平面区域(含边界)为D。若曲线x2-2ax+y2-4y+a2+
正确答案
解析
曲线x2-2ax+y2-4y+a2+
其圆心坐标为E(a,2),半径r=
由图可知,当0≤a≤
当a<0时,要圆与点D有公共点,只需圆心到直线l:x-y+2=0的距离d=

得-

知识点
8.抛物线y=x2与直线x-y+2=0构成封闭平面区域(含边界)为D。若曲线x2-2ax+y2-4y+a2+
正确答案
解析
曲线x2-2ax+y2-4y+a2+
其圆心坐标为E(a,2),半径r=
由图可知,当0≤a≤
当a<0时,要圆与点D有公共点,只需圆心到直线l:x-y+2=0的距离d=

得-

知识点
22.选修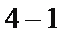
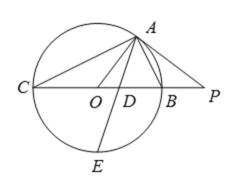
如图所示,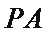

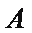


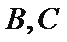
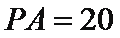



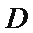
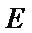
(Ⅰ)求证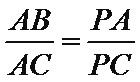
(Ⅱ)求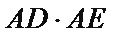
正确答案
(1)见解析;(2)
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
(1)由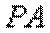
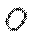
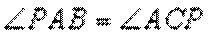
又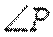
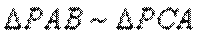
(2)由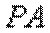
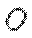
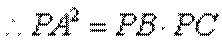
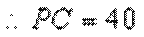
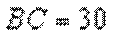
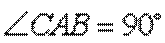
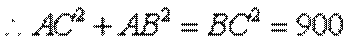
又由(1)知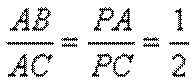
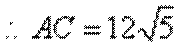
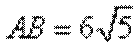
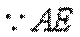
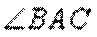
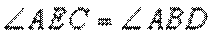
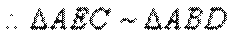
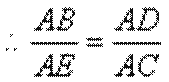
考查方向
解题思路
(1)利用相似三角形即可得证;
(2)利用切割线定理即可求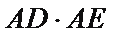
易错点
相关定理不熟悉导致本题失分。
知识点
扫码查看完整答案与解析