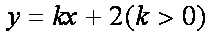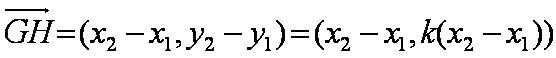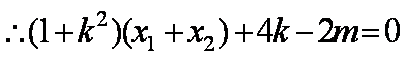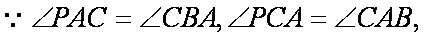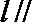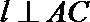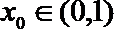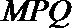- 两圆的公切线条数及方程的确定
- 共94题
下列函数中,既是奇函数又是增函数的为( )
正确答案
解析
对于A,非奇非偶,是R上的增函数,不符合题意;
对于B,是偶函数,不符合题意;
对于C,是奇函数,但不是增函数;
对于D,令f(x)=x|x|,∴f(﹣x)=﹣x|﹣x|=﹣f(x);∵f(x)=x|x|=
∴ 函数是增函数
故选D。
知识点
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是地面边长的

(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P-AC-D的大小
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。
正确答案
见解析
解析
(1)连BD,设AC交BD于O,由题意SO⊥AC。
在正方形ABCD中,AC⊥BD,所以AC⊥平面SBD,
得AC⊥SD。
(2)设正方形边长a,则SD=
又OD=

连OP,由(1)知AC⊥平面SBD,所以AC⊥OP,且AC⊥OD,所以

即二面角P-AC-D
(3)在棱SC上存在一点E,使BE//平面PAC
由(2)可得PD=

(1)连BD,设AC交于BD于O,由题意知SO⊥平面ABCD,
以O为坐标原点,
建立坐标系O-xyz如图。设底面边长为a,则
(2)由题意知面PAC的一个法向量为

由(2)知

知识点
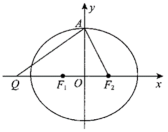
已知椭圆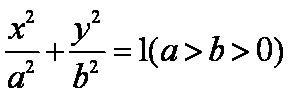

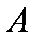


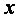
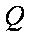
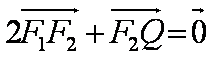

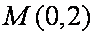


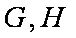


(1)求椭圆的标准方程;
(2)设直线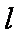
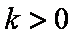
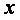

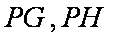

正确答案
见解析
解析
(1)
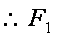
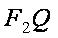

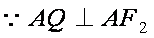
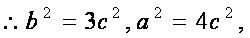
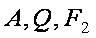
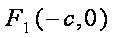

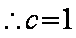
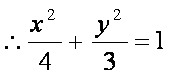
(2)设直线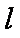
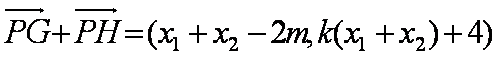
由于菱形对角线垂直,则
解得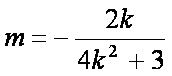
即

当且仅当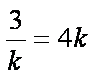
知识点
以直角坐标系的原点O为极点,x轴的正半轴为极轴,已知点P的直角坐标为(1,-5),点M的极坐标为(4,),若直线l过点P,且倾斜角为
(1)求直线l关于
(2)试判定直线l和圆C的位置关系。
正确答案
见解析。
解析
(1)直线l的参数方程为
圆C的极坐标方程为
(2)因为
直线l的普通方程为
∴圆心到直线l的距离
所以直线l与圆C相离。
知识点
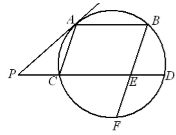
如图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E 、交圆于F,过A点的
切线交DC的延长线于P,PC=ED=1,PA=2。
(1)求AC的长;
(2)试比较BE 与EF 的长度关系。
正确答案
(1)AC=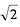
解析
(1)

又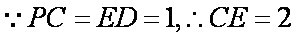
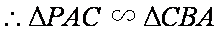
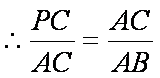

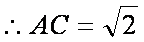
(2)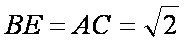
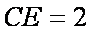
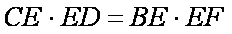

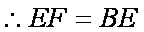
知识点
10.在平面直角坐标系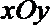
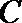
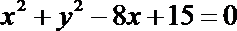

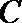
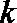
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 在数列



(Ⅰ)证明:数列
(Ⅱ)求
(Ⅲ)求数列


正确答案
(Ⅰ) 
由定义知数列
(Ⅱ)因为数列
则
(Ⅲ) 
解析
解析已在路上飞奔,马上就到!
知识点
8.设随机变量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
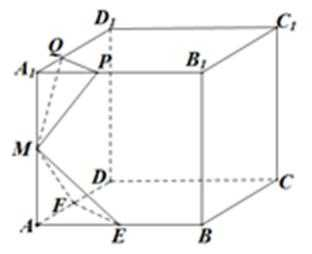
7.已知棱长为1的正方体



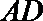
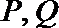
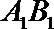

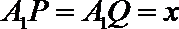

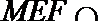
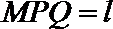
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数




正确答案

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析