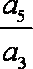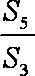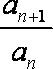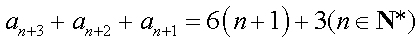- 函数的定义域及其求法
- 共105题
设定义域为


(1)求
(2)请你选定一个区间


正确答案
见解析
解析
解析:(1)由题意,对于任意的

即,

所以,
另解:对任意的



设


所以,对任意的

有

故,

又,对任意的

有

故,

对于任意的

故,当

因为方程

(2)选定




知识点
设等比数列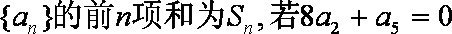
正确答案
解析
等比数列{an}满足8a2+a5=0,即a2(8+q3)=0,∴q=-2,∴=q2=4,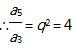
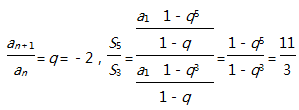
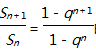
知识点
已知定义在




正确答案
解析
由题
故


记
且
故方程
知识点
已知数列
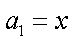
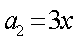
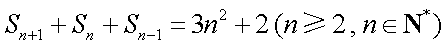
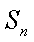
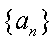
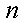
(1)若数列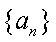
(ⅰ)求数列的通项
(ⅱ)若数列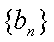
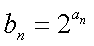
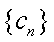
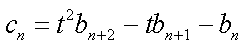
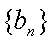
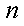
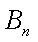
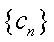
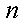

(2)若对任意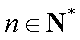
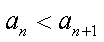

正确答案
见解析。
解析
(1)(ⅰ)因为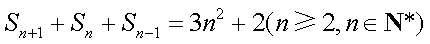
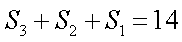
即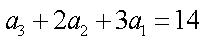
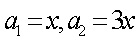
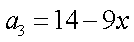
又因为数列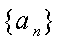
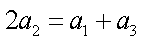

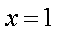
所以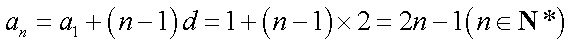
(ⅱ)因为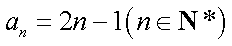

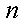

又因为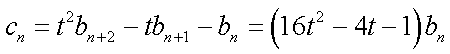
所以其前
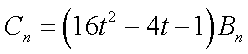
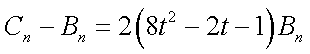
当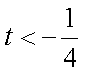
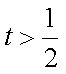

当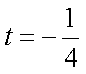
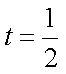
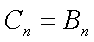
当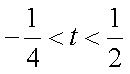
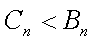
(2)由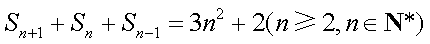
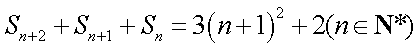
两式作差,得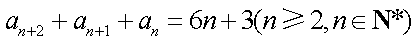
所以
再作差得
所以,当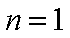
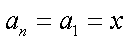
当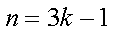
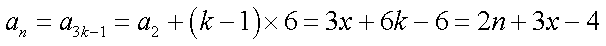
当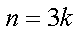

当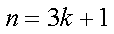
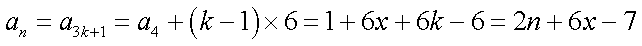
因为对任意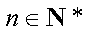
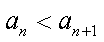
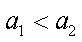
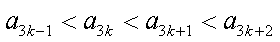
所以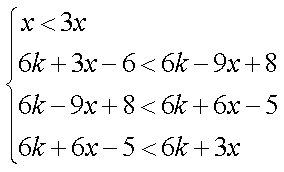
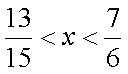
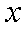
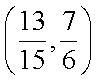
知识点
已知定义在




正确答案
解析
由题

故


记

且
故方程
知识点
扫码查看完整答案与解析