· 三角恒等变换

· 两角和与差的正弦函数

两角和与差的正弦函数
共73题

· 三角恒等变换

· 两角和与差的正弦函数

两角和与差的正弦函数
共73题

热门试卷

X 查看更多试卷

1

题型：简答题

|

简答题 · 12 分

16．已知函数.

（Ⅰ）求函数的最大值，并写出取最大值时的取值集合；

（Ⅱ）已知中，角的对边分别为若求实数的最小值.

正确答案

(Ⅰ)

.

∴函数的最大值为.要使取最大值，则

，解得.

故的取值集合为.

（Ⅱ）由题意，，化简得

，，∴， ∴

在中，根据余弦定理，得.

由，知，即.

∴当时，实数取最小值

解析

解析已在路上飞奔，马上就到！

知识点

两角和与差的正弦函数二倍角的余弦余弦定理三角函数的最值

1

题型：简答题

|

简答题 · 12 分

18．设函数f(x)=2在处取最小值.

（1）求的值;

（2）在ABC中,分别是角A，B，C的对边，已知,求角C.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两角和与差的正弦函数二倍角的正弦二倍角的余弦余弦定理

1

题型：简答题

|

简答题 · 12 分

18.在中，三个内角，，的对边分别为，，，其中，且

（1）求证：是直角三角形；

（2）设圆过三点，点位于劣弧上，，用的三角函数表示三角形的面积，并求面积最大值.

正确答案

（1）证明：由正弦定理得，整理为，

即sin2A＝sin2B ∴2A＝2B或2A＋2B＝π,

即A＝B或A＋B＝∵，∴A＝B舍去.

由A＋B＝可知c＝，∴ΔABC是直角三角形

（2）由（1）及，得，

在RtΔ中，

所以，

，

因为，所以，，

当，即　时，最大值等于

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域两角和与差的正弦函数正弦定理

1

题型：简答题

|

简答题 · 12 分

19.在中，的对边分别为且成等差数列．

（1）求的值；

（2）求的范围．

正确答案

（1）由正弦定理得，，

即：，．

又在中，， .

（2），所以

，

的范围是

解析

解析已在路上飞奔，马上就到！

知识点

三角函数中的恒等变换应用两角和与差的正弦函数正弦定理等差数列的性质及应用

1

题型：单选题

|

单选题 · 5 分

8．已知sinα－sinβ＝,cosα－cosβ＝，则等于（）

A

B

C

D

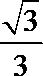
正确答案

A

解析

知识点

同角三角函数间的基本关系三角函数的化简求值两角和与差的正弦函数二倍角的余弦

继续学习学习下一知识点

下一知识点 : 两角和与差的正切函数

百度题库 > 高考 > 理科数学 > 两角和与差的正弦函数

扫码查看完整答案与解析