两角和与差的正弦函数
共73题

· 两角和与差的正弦函数

两角和与差的正弦函数
共73题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 10 分

17．已知.

（1）求的值；

（2）求的值.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的化简求值弦切互化两角和与差的正弦函数二倍角的余弦二倍角的正切

题型：填空题

填空题 · 5 分

14．若关于的方程在区间上有两个不同的实数解，则的取值范围为。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的图象正弦函数的定义域和值域两角和与差的正弦函数

题型：填空题

填空题 · 5 分

4．在中,，则（）

正确答案

或

解析

解析已在路上飞奔，马上就到！

知识点

同角三角函数间的基本关系三角函数的化简求值诱导公式的作用两角和与差的正弦函数

题型：填空题

填空题 · 5 分

4.计算：＝_________。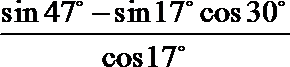

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的化简求值两角和与差的正弦函数角的变换、收缩变换

题型：简答题

简答题 · 12 分

18．已知的两边长分别为，，且O为外接圆的圆心。（注：，）

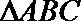
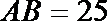
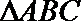
（1）若外接圆O的半径为，且角B为钝角，求BC边的长；

（2）求的值

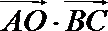
正确答案

（1）由正弦定理有，

∴，

∴，，

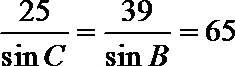
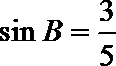
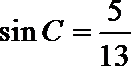
且B为钝角，

∴，，

∴，

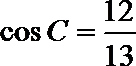
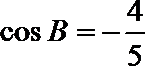
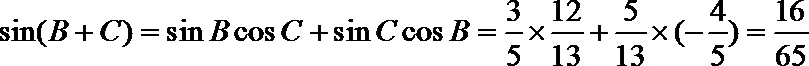
又，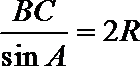

∴；

（2）由已知，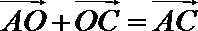

∴，

即

同理，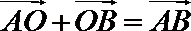

∴，

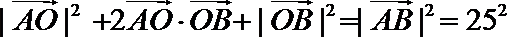
两式相减得，

即，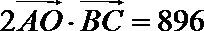

∴．

解析

解析已在路上飞奔，马上就到！

知识点

同角三角函数间的基本关系两角和与差的正弦函数正弦定理平面向量数量积的运算

题型：单选题

单选题 · 5 分

1.已知（sin+cos）=-,则sin β的值为（　　）.

B-

D-

正确答案

解析

两边平方,得(1+sin β)=,∴sin β=

知识点

三角函数的化简求值两角和与差的正弦函数二倍角的余弦角的变换、收缩变换

题型：单选题

单选题 · 5 分

2．的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的恒等变换及化简求值诱导公式的作用两角和与差的正弦函数

题型：简答题

简答题 · 3 分

8．已知，则

正确答案

解析

由题可知，sina=3/5，可求得cosa=4/5,所以。

考查方向

本题主要考查了两角和差公式和诱导公式

解题思路

本题考查两角和差公式和诱导公式，解题步骤如下：利用两角和差公式和诱导公式求解。

易错点

本题要注意诱导公式。

知识点

同角三角函数间的基本关系三角函数的化简求值诱导公式的作用两角和与差的正弦函数

题型：填空题

填空题 · 4 分

14．已知是锐角的外心，．若，则实数___________．

正确答案

解析

如图所示，设的中点，连，

由三角形外接圆的性质可得，

∴．

∵，代入已知得

，

两边与作数量积得

，

∴

由正弦定理可得

化简得

又∵

∴，即

又∵

∴

∴．

考查方向

本题综合考查了三角形外接圆的性质、垂径定理、正弦定理、数量积运算性质、两角和差的余弦公式、三角函数基本关系式等基础知识与基本技能方法，考查了分析问题和解决问题的能力，属于难题．这类问题在近几年各省市的高考试卷中出现频率很高，以平面向量为载体，可以与三角、函数、数列、解析几何等知识结合交汇命题．

解题思路

取的中点，连，由三角形外接圆的性质可得，于是．

由向量的三角形法则可得，代入已知，两边与作数量积得到，

再利用正弦定理化简可得，再利用两角和差的余弦公式和三角函数的基本关系式即可得到．

易错点

对条件的不理解，综合运用各种知识解决问题．

知识点

两角和与差的正弦函数正弦定理向量的加法及其几何意义平面向量数量积的运算

题型：填空题

填空题 · 5 分

12．已知，，且，则sinβ=　　　．

正确答案

解析

考查方向

本题主要考查了同角三角函数的基本关系、两角差的正弦公式，以及三角函数在各个象限中的符号判断等知识，意在考查“凑角思想”的应用，在近几年的各省高考题出现的频率较高，常是三角公式与三角函数等知识交汇命题，较难。

解题思路

1、先根据题意构造sinβ=sin[（α+β）﹣α]。

2、由两角差的正弦公式得出结论。

易错点

1、本题在构造sinβ=sin[（α+β）﹣α]时易出错。

知识点

两角和与差的正弦函数角的变换、收缩变换

继续学习学习下一知识点

下一知识点 : 两角和与差的正切函数

百度题库 > 高考 > 理科数学 > 两角和与差的正弦函数

扫码查看完整答案与解析