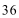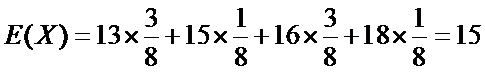- 极差、方差与标准差
- 共27题
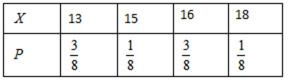
10.若数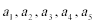
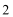
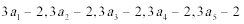
正确答案
36
解析
∵数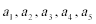
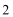
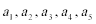
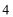
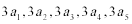
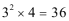
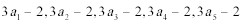
考查方向
本题考查了概率与统计中的方差与标准差.
解题思路
先求数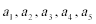

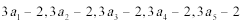
易错点
直接利用方差与标准差的公式计算,计算量大并且容易出错,如果利用新旧两组数据方差之间的关系,可以减少错误.
知识点
6.气象意义上从春季进入夏季的标志为:“连续



①甲地:


②乙地:


③丙地:



则肯定进入夏季的地区有( )
正确答案
解析
由题可知,乙地、丙地的数据符合夏季的标志,甲地不符合。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查统计
解题思路
1、分析三地的温度情况;
2、按照条件判断,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在判断语意时发生错误。
知识点
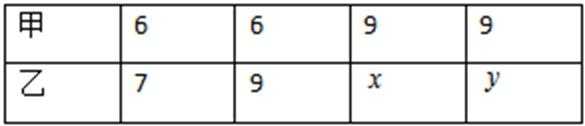
16.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分。 两人4局的得分情况如下:
(Ⅰ)若从甲的4局比赛中,随机选取2局,求这2局的得分恰好相等的概率;
(Ⅱ)如果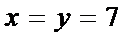
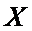
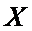
(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出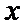
正确答案
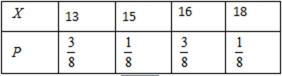
(Ⅰ)
(Ⅱ)
(Ⅲ)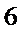

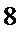
解析
试题分析:本题属于概率与统计的基本问题,题目的难点是逐渐由易到难,(1)直接按照步骤来求,(2)要注意正确求出每个变量对应的概率,(3)要注意利用离散型随机变量的分布列的性质验证分布列的正确性。
(Ⅰ)解:记 “从甲的4局比赛中,随机选取2局,且这2局的得分恰好相等”为事件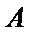
由题意,得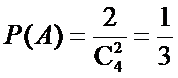
所以从甲的4局比赛中,随机选取2局,且这2局得分恰好相等的概率为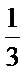
(Ⅱ)解:由题意,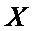
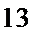
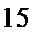
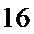

且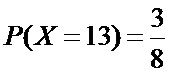
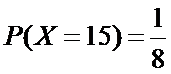
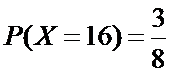
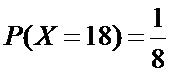
所以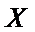
所以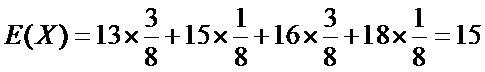
(Ⅲ)解: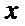
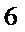
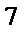
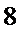
考查方向
本题主要考查了离散型随机变量的分布列、期望与方差,离散型随机变量的分布列大体有以下几类:
1.两点分布,
2.二项分布,超几何分布.
解题思路
本题考查离散型随机变量的分布列、期望与方差,解题步骤如下:
1.利用古典概型的概率公式进行求解;
2.写出随机变量的所有可能取值,分别求出每个变量对应的概率;
3.列表得到随机变量的分布列;
4.根据数学期望公式求其期望;
5.列出可能取值。
易错点
第二问中每个随机变量的概率不完全正确,导致结果错误。
知识点
10.若数

则数
正确答案
6
解析
方差是标准差的平方,
所以
因为若数据

则数据

所以数
它们的标准差为6.
考查方向
解题思路
本题考查标准差的求法,注意利用公式求解求解的能力,解题步骤如下:先将已知变量标准差转化为方差,求所求变量的方差,再求其标准差。
易错点
本题必须注意区分方差、标准差,忽视则会出现错误。
知识点
4.若样本数据








正确答案
16
解析
2*8=16
考查方向
解题思路
本题考查采用标准差与数据关系的结论:只与系数相关。解题步骤如下:2*8=16
易错点
本题必须注意标准差含义,忽视则会出现错误。
知识点
扫码查看完整答案与解析