- 二元二次方程表示圆的条件
- 共80题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种家和品种乙)进行田间试验,选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙。
(1)假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列和数学期望;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据x1,x2,…,xa的样本方差s2=




正确答案
见解析
解析
(1)由题意知X的可能取值是0,1,2,3,4,
P(X=0)=
P(X=1)=
P(X=2)=
P(X=3)=
P(X=4)=
∴X的分布列为
∴X的期望是
(2)品种甲的每公顷产量的样本平均数

方差是
品种乙每公顷的产量的样本平均数

方差是
有以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,
且两个品种的样本方差差异不大,故应选择种植品种乙。
知识点
如图,已知椭圆C1的中心在原点O,长轴左、右端点M,N在x轴上,椭圆C2的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C2交于两点,这四点按纵坐标从大到小依次为A、B、C、D。
(1)e=
(2)当e变化时,是否存在直线l,使得BO∥AN,并说明理由。
正确答案
见解析
解析
(1)因为C1,C2的离心率相同,
故依题意可设
设直线l:x=t(|t|<a),分别与C1,C2的方程联立,
求得

当

可知
(2)t=0时的l不符合题意,t≠0时,
BO∥AN当且仅当BO的斜率kBO与AN的斜率kAN相等,
即
解得
因为|t|<a,又0<e<1,所以
所以当
当
知识点
15.椭圆






正确答案
解析
根据椭圆定义知:4a=12, 得a=3 , 又
知识点
设全集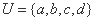
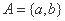
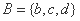

正确答案
{a, c, d}
解析
∵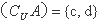
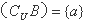

知识点
扫码查看完整答案与解析













