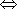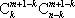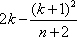- 二元二次方程表示圆的条件
- 共80题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有n位学生,每次活动均需该系k位学生参加(n和k都是固定的正整数),假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系k位学生,且所发信息都能收到,记该系收到李老师或张老师所发活动通知信息的学生人数为X.
(1)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(2)求使P(X=m)取得最大值的整数m.
正确答案
(1) 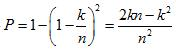
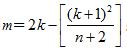
解析
(1)因为事件A:“学生甲收到李老师所发信息”与事件B:“学生甲收到张老师所发信息”是相互独立的事件,所以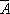
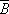
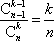
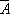
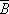
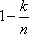
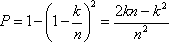
(2)当k=n时,m只能取n,有P(X=m)=P(X=n)=1.
当k<n时,整数m满足k≤m≤t,其中t是2k和n中的较小者。
由于“李老师和张老师各自独立、随机地发活动通知信息给k位同学”所包含的基本事件总数为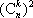
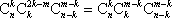
此时P(X=m)=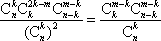
当k≤m<t时,P(X=m)≤P(X=m+1)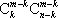
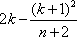
假如k≤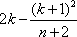
k≤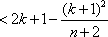
故P(X=m)在m=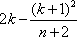
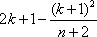
当(k+1)2不能被n+2整除时,
P(X=m)在m=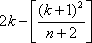
(注:[x]表示不超过x的最大整数)
下面证明k≤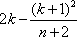
因为1≤k<n,所以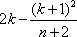
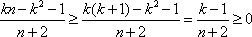
而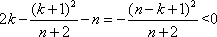
故2k-<n.
显然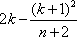
因此k≤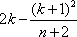
知识点
设抛物线








(1)若




(2)若






正确答案
(1)

(2)坐标原点到
解析
(1)由对称性知:

点

圆
(2)由对称性设
点

得:

直线
坐标原点到

知识点
如图,在四棱柱







(1)求证:
(2)若直线



(3)现将与四棱柱


正确答案
见解析
解析
(1)
取





在









(2)以





所以

设平面

得

设





(3)共有
知识点
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D。
(1)证明:DB=DC;
(2)设圆的半径为1,BC=
正确答案
见解析
解析
(1)
连结DE,交BC与点G.
由弦切角定理得,∠ABF=∠BCE,∵∠ABE=∠CBE,∴∠CBE=∠BCE,BE=CE,
又∵DB⊥BE,∴DE是直径,∠DCE=
(2)由(Ⅰ)知,∠CDE=∠BDE,BD=DC,故DG是BC的中垂线,∴BG=
设DE中点为O,连结BO,则∠BOG=

∴CF⊥BF, ∴Rt△BCF的外接圆半径等于
知识点
设数列|an|的前n项和Sn满足Sn+1=a2Sn+a1,其中a2≠0。
(1)求证:|an|是首项为1的等比数列;
(2)若a2>﹣1,求证:
正确答案
见解析
解析
(1)∵ Sn+1=a2Sn+a1,①
∴ Sn+2=a2Sn+1+a1,②
①﹣②可得:an+2=a2an+1
∵ a2≠0,∴
∵ Sn+1=a2Sn+a1,∴S2=a2S1+a1,∴ a2=a2a1
∵ a2≠0,∴a1=1
∴ {an}是首项为1的等比数列;
(2)当n=1或2时,
设n≥3,a2>﹣1,且a2≠0,由(I)知a1=1,

即证
a2=1时,等号成立
当﹣1<a2<1时,

当a2>1时,

∴ a2>﹣1且a2≠1时,(

上面不等式n分别取1,2,…,n累加可得
∴
综上,
知识点
已知



正确答案
解析
知识点
已知某一多面体内接于一个简单组合体,如果该组合体的正视图,测试图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________
正确答案
解析
由图可知,图形为一个球中间是内接一个棱长为2的正方体,
知识点
已知函数





(1)求函数

(2)是否存在


(3)求实数



正确答案
(1)






解析
(1)由函数


又曲线

故

将函数




(2)当

所以
问题转化为方程

设
则
因为



又
且函数



即存在唯一的
(3)依题意,
当







现研究
令
则问题转化为研究直线





当


当



当



当



当



故当





当





当






由函数















综上,当




知识点
如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1,l2之间,l∥l1,l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点,设弧
正确答案
解析
略
知识点
扫码查看完整答案与解析